First-order reactions are those in which their rate is directly proportional to the concentration of a single reactant. In this article, we will look at the equations for a first-order reaction and also look at diagrams that illustrate this relationship
- This article covers first-order reactions
- First, we will look at the definition of a first-order reaction
- Next, we will derive the related formulas for the reactions and see what the graphs of these equations look like
- Lastly, we will derive the formula for half-life
First-order Reaction Definition
The order of a reaction is the relationship between the concentration of a reactant or reactants and the rate. The relationship can be linear, quadratic, or no relationship exists.
A first-order reaction is a reaction where the rate is dependent on the concentration of only one reactant. Because of this, it is also called a unimolecular reaction. The rate equation for this type of reaction is:
\(rate=k[A]\)
Where, k, is the rate constant (constant showing proportion between concentration and rate) and, [A], is the concentration of the reactant, A.
Since first-order reactions depend solely on the concentration of one reactant, they are often decomposition reactions. A decomposition reaction is where one reactant breaks down into two or more simpler species. A general reaction looks like this:
\(A \rightarrow B + C\)\(\text{rate}=k[A]\)
One thing to keep in mind is that first-order reactions are not always one reactant-dependent reactions. It just means that the reaction rate is only dependent on the concentration of one of the reactants.
First-order Reaction Example
First, let's look at an example of your "typical" first-order reaction:
\(CaCO_{3\,(s)} \rightarrow CaO_{(s)} + CO_{2\,(g)}\)
\(\text{rate}=k[CaCO_3]\)
This is an example of a decomposition reaction. Like we said before, first-order reactions can have more than one reactant. Here is an example:
\((CH_3)_3CBr_{(aq)} + H_2O_{(l)} \rightarrow (CH_3)_3COH_{(aq)}\)
\(\text{rate}=k[(CH_3)_3CBr]\)
In this reaction, the rate is independent of the concentration of water, so it is a first-order reaction. This is because the concentration of water is so much higher than, (CH3)3CBr, so that the change in the concentration of water is negligible.
A second thing to remember is that not all reactions that have one reactant are first-order. Here is another example:
\(2N_2O_{(g)} \underset {\text{highpressure}} {\stackrel {\text{hot Pt}} {\longrightarrow}} 2N_{2\,(g)} + O_{2\,(g)} \)
\(\text{rate}=k\)
Here, this reaction is completely independent of the reactant concentration, so it is a zero-order reaction. Normally, this reaction is first-order, however, under these special conditions (reaction is done on a hot Pt plate at high pressure) it is zero-order. These types of reactions are the exception to the rule, but it is important to keep them in mind.
First-order Reaction Units
For each different "reaction order", the rate constant has different units. The units for the rate of reactions are always, M/s (molarity/second). This is because we are tracking a change in concentration (molarity) over time. In a first-order reaction the reaction constant, k, is in units of per second, 1/s. Here is how we get those units:
\(\text{rate}=k*[A]\)
In what follows, we will write out the names of the dimensional units in square brackets. Thus, for a first-order reaction, we will have:
\(rate\frac{[Molarity]}{[seconds]}={k}[unknown]*[A][Molarity]\)
where, [Molarity], refers to the dimension of molarity, [seconds], refers to the dimension of seconds, and [unknown], refers to the dimension that we want to determine. Notice, as before, [A], is the symbol for the concentration of the species, A. Then, to have the same dimensional units on both sides of the equation we would need the unknown dimensions of the rate constant, k, to have units of one over seconds, thus:
\(rate\frac{[Molarity]}{[seconds]}={k}[\frac{1}{seconds}]*[A][Molarity]\)
Note that, k, will have the same dimensional units, no matter what form the first-order rate equation is in. As long as we are working with a first-order reaction, k will be in units of 1/s. Also, remember that molarity is, M = mols/L.
First-order Reaction Equation
The equation we saw earlier is the basic form of the rate equation, but there are two other versions that are important. First, let's walk through the derivation of the first equation we discussed:
\(\text{rate}=-\frac{d[A]}{dt}=k[A]\)
\(\frac{d[A]}{[A]}=-kt\)
Here \(-\frac{d[A]}{dt}\) is an expression that means "change in [A] over time". It is the expression for a derivative.
The next few steps involve integration. You won't need to worry about the math, this is just to show you where the equation comes from. Beginning from the beginning, we start with the formula for the rate:\(-\frac{d[A]}{dt}=k[A]\)
Then rearranging we get:
\(\frac{d[A]}{[A]}=-kdt\)
Now, we integrate both sides:
\(\int_{[A]_0}^{[A]} \frac{d[A]}{[A]}=-\int_{0}^{t} kdt \,\,\text{(the integral is from the initial to final value of the variable)}\)
\( \int \frac{1}{x}=ln(x)\,\,\text{(the form we use to evaluate the integral)}\)
Using this integration rule, we get:
\(\ln[A]-ln[A]_0=-kt\)\(\ln[A]=-kt+ln[A]_0$\)
Where, [A], is the concentration of the reactant, A, the initial concentration of the species is, [A]0, the rate constant is, k, the time is, t, and the symbol for the natural logarithm is ln. So, this equation shows us how much of a reactant we will have left after a given time. You'll notice that this reaction equation is in the form of the equation of a line (y = mx+b). This shows that the relationship between the natural log of the species, ln[A], and the rate constant, k, is inversely proportional (i.e. as one goes up, the other goes down).
Now onto the second form of the equation. Returning to the the first-order reaction equation we just derived:
\(\ln[A]=-kt + ln[A]_0\)
We exponentiate both sides:
\(e^{ln[A]}=e^{-kt+ln[A]_0}\)
Note, the following rule exponentiation rules:\(e^{x+y}=e^xe^y\,\,\text{(the form we use to solve the exponential)}\)
\(e^{ln(x)}=x\,\,\text{(substitution we will use)}\)
Thus,
\(e^{ln[A]}=e^{-kt}e^{ln[A]_0}\)
\([A]=[A]_0e^{-kt}\)
In this form, we see that the relationship between concentration and rate is exponential. This demonstrates the same inversely proportional relationship as before.
First-order Reaction Graph
Now that we have derived our equations, we can graph them. Let's start with the graph for the second equation, \([A]=[A]_0e^{-kt}\)
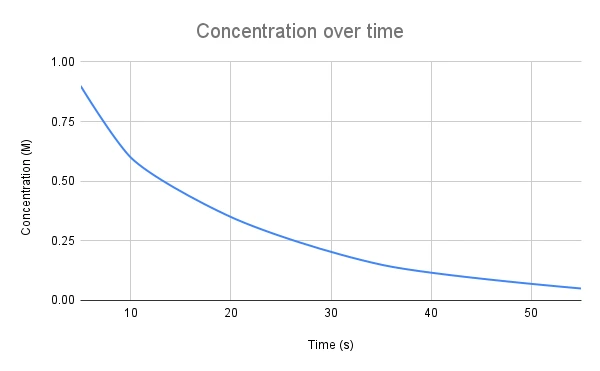
Fig. 1. In a first-order reaction, the graph of concentration over time is a downward curve.
The graph is a downward curve, which makes sense since the concentration of a reactant will decrease over time as the product(s) is formed. Since we can't easily calculate the rate constant from this graph, it is more commonly used as a way to identify the order of a reaction if it is unknown. Only first-order reactions will have this shape when the concentration change over time is graphed.
Now for the first equation: \(ln[A]=-kt+ln[A]_0\)
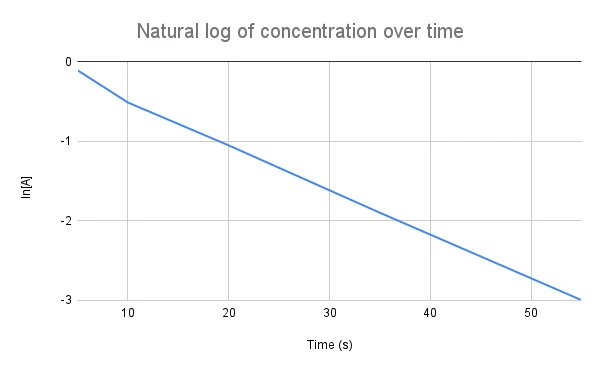
Fig. 2. First-order reactions have a linear relationship between the natural log of the concentration and time.
This graph is more helpful since the slope is just the negative rate constant, -k. By setting up this graph, we can easily determine the rate constant. Only first-order reactions have a linear relationship between the natural log and the concentration, ln[A], and the time, t.
As mentioned previously, we can use this graph to calculate our rate constant, k. Let's walk through an example of this:
Given the graph below, what is the value of the rate constant? What is the concentration of the reactant at 60 seconds?
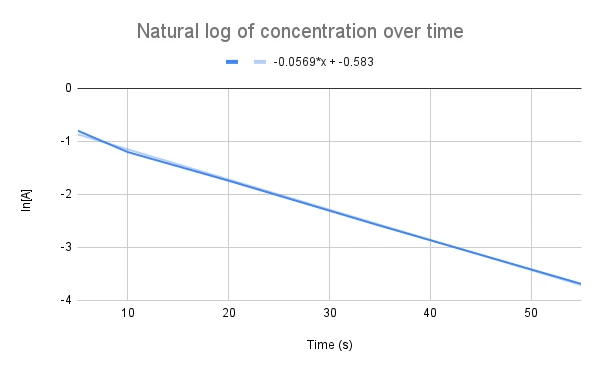
Fig. 3. Natural log of concentration over time sample data.
From the graph, we are given the linear equation, \(y=-0.0569x - 0.583\). Based on our equation, we know that the slope is equal to -k, which means that, k = 0.0569 s-1.
Now for the second question, "what is the concentration of the reactant at 60 seconds?" All we need to do is plug in our value for the time, t, using the equation of the line and solve for concentration.
\(ln[A]=-kt+ln[A]_0\)\(y=-0.0569x-0.583\)
\(ln[A]=-0.0569s^{-1}t-0.583\)\(ln[A]=-0.0569s^{-1}(60\,s)-0.583\)\(ln[A]=-3.997\)\(e^{ln[A]}=e^{-3.997}=0.0184\)
Thus, by appending the dimensions of molarity, M, to the answer, we get:
\([A]=0.0184\,M\,\,\text{(While ln terms are dimensionless, concentration terms will always be in M)}\)
In that example, we were given the equation of the line, but what about if we are given raw data?
Given the data below, calculate the rate constant
| [A] | ln[A] | time, t |
| 0.225 M | -1.49 | 5 s |
| 0.150 M | -1.90 | 10 s |
| 0.075 M | -2.59 | 20 s |
| 0.0375 M | -3.28 | 35 s |
| 0.0125 M | -4.38 | 55 s |
Since we know that the rate constant is equal to the negative slope, we can pick any two points (time, ln[A]) and plug them into the equation for slope:\(\text{slope}=\frac{y_2-y_1}{x_2-x_1}\)\(-k=\frac{ln[A]_2-ln[A]_1}{t_2-t_1}\)\(\text{points}: (5\,s,-1.49)\,and\,(55\,s,-4.38)\)\(-k=\frac{-4.38-(-1.49)}{55\,s-5\,s}\)\(-k=-0.0578\,s^{-1}\)\(k=0.0578\,s^{-1}\)
Half-life for First-order Reactions
Since first-order reactions are typically decomposition reactions, it is common to calculate and use the half-life.
The half-life of a species is the time when the current concentration is half its original value. The general formula is:\([A]=\frac{1}{2}[A]_0\)
Let's derive the formula. First, we are going to use our integrated rate law and move all concentration variables to one side:
\([A]=[A]_0e^{-kt}\)
\(\frac{[A]}{[A]_0}=e^{-kt}\)
Now let's look at our basic half-life equation. We need to move all concentration variables to one side so we can substitute this expression into our other equation.
\([A]=\frac{1}{2}[A]_0\)
\(\frac{[A]}{[A]_0}=\frac{1}{2}\)
Now we can substitute this expression into our first equation and solve for t (half-life).
\(\frac{1}{2}=e^{-kt}\)\(ln(\frac{1}{2})=ln(e^{-kt})\)\(-0.693=-kt\)\(t_\frac{1}{2}=\frac{0.693}{k}\)
So, the half-life doesn't depend on the concentration, only on the rate constant.
If it takes 112 seconds for species A to decompose from 0.6 g to 0.3 g, what is the rate constant? (Assume it is a first-order reaction)
Since the half-life doesn't depend on the concentration, we just need to plug in the time value into the equation to solve for k:
\(t_{\frac{1}{2}}=\frac{0.693}{k}\)\(112\,s=\frac{0.693}{k}\)\(112\,s \cdot k=0.693\)\(k=6.19X10^{-3}\,s^{-1}\)
Carbon dating utilizes the half-life of 14C to determine the age of an organic object. The decay of carbon-14 is a first-order reaction, so the half-life of carbon-14 was calculated using that equation. The formula for determining an object's age using carbon dating is:
\(t=\frac{(ln(\text{percent of carbon-14)}}{-0.693}*5,700\,yrs\)
The percent of carbon-14 left is determined by comparing the concentration to a living sample. For example, if a fossil had 15% of its carbon-14 left:
\(t=\frac{ln(0.15)}{-0.693}*5,700\,yrs\)
\(t=15,604\,yrs\)
First Order Reaction - Key takeaways
- A first-order reaction is a reaction where the rate is dependent on the concentration of only one reactant. Because of this, it is also called an unimolecular reaction.
- The units of the rate constant for a first-order reaction is 1/s. The first derived form of the rate equation is: \(ln[A]=-kt+ln[A]_0\). When the change in ln[A] over time is graphed, the graph will be linear and the slope is equal to -k
- The second derived form of the rate equation is: \([A]=[A]_0e^{-kt}\) When the change in concentration over time is graphed, the graph will be a downward curve.
- The half-life of a species is the time when the current concentration is half its original value. For a first-order reaction, the equation for the half-life is: \(t_{\frac{1}{2}}=\frac{0.693}{k}\)
Similar topics in Chemistry
Related topics to Kinetics










