Common Ion Effect Definition
Let's begin by looking at the definition of Le Chatelier's principle, and at the definition of common ion effect.
Le Chatelier’s principle states that when a chemical system at equilibrium suffers a sudden change in concentration, volume, temperature, and/or pressure that causes it to shift away from equilibrium, this change is, in turn, counteracted by the system in a way that re-establishes equilibrium.
Le Chatelier’s principle and the common ion effect are directly related. To understand the common ion effect, we must first understand Le Chatelier’s principle. Above, we’ve written the basic importance and definition of Le Chatelier’s principle for this very reason.
To facilitate an even better understanding of this article, we will go over the basics of Le Chatelier below:
Disturbance in this case means a change in the system’s conditions. Which include:
change in temperature by cooling or heating
change in concentration by adding or removing a reactant/product
change in pressure by adding a gas or decreasing the volume of a reaction
The chemical equilibrium we refer to is the overall net reaction. When a reaction is in equilibrium, the reaction rate of the reactants and products are equivalent.
If a reaction is not in equilibrium, then Le Chatelier states that the reaction will shift back to equilibrium by adjusting the concentrations of reactants or products in order to re-establish the equilibrium ratio.
- When we increase the concentration of the reactants, the equilibrium shifts to the right and the forward reaction is favored, resulting in more product being made until equilibrium is reached again.
- When we increase the concentration of the products, the equilibrium shifts to the left and the backward reaction is favored, resulting in more reactants being made until equilibrium is reached again.
This is just a quick rundown of Le Chatelier’s principle, for a more in-depth understanding please reference our “Le Chatelier’s Principle” article.
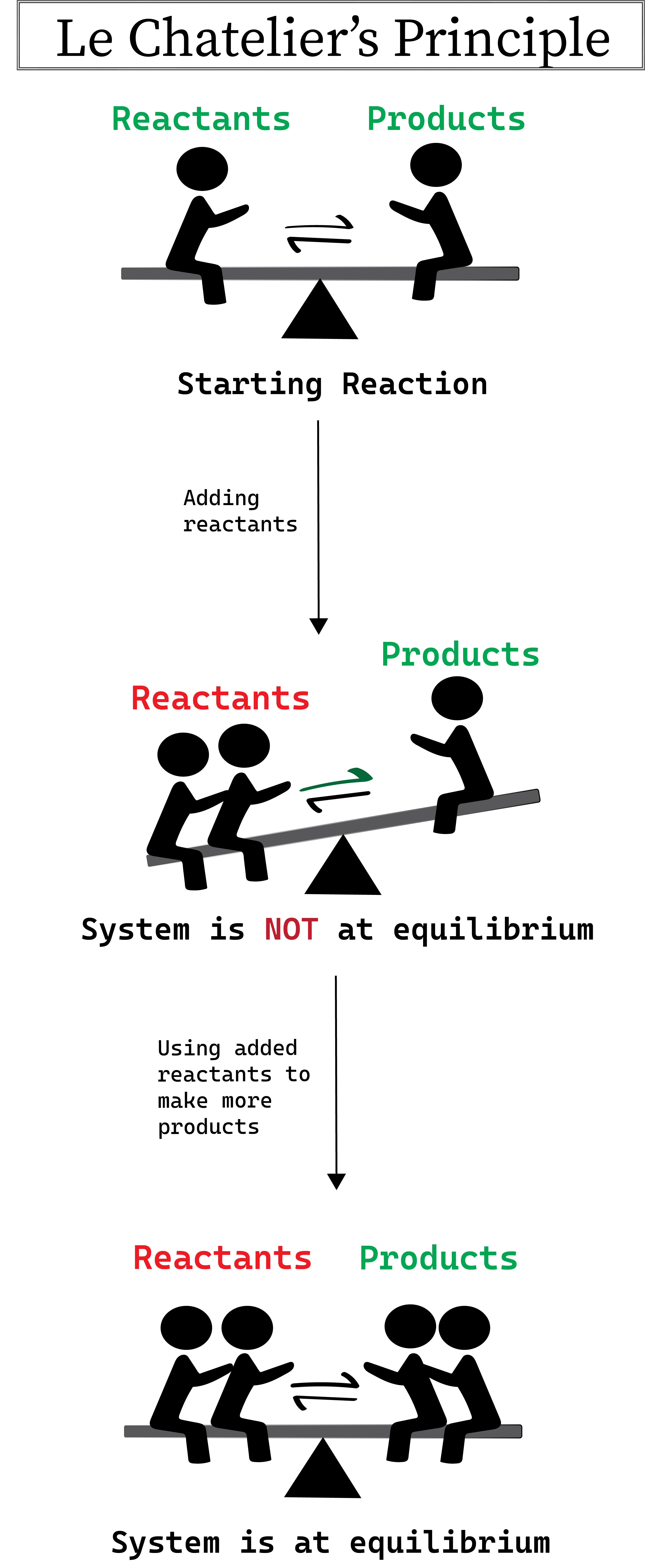
Figure 1: Le Chatelier's Principle illustrated. Daniela Lin, Study Smarter Originals.
In the illustration above, increasing the reactants causes a shift in the equilibrium to the other side until the balance is re-established by the production of more products. Keep in mind that if we were to add more products instead of reactants the equilibrium would shift towards the products until more reactants are made to re-establish balance.
Now that we’ve had a brief look at Le Chatelier’s principle, we can move on to defining our common ion effect.
The common ion effect is a shift in equilibrium caused by the addition of an ion that’s already involved in the reaction.
Common Ion Effect on Solubility
Since we’ve defined the common ion effect as a shift in equilibrium, the next question to ask would be how does this shift in equilibrium affect our reaction?
The simple answer to that would be that the shift in equilibrium caused by adding a common ion impacts solubility.
This is because when we add a common ion, the reaction shifts towards the reactants (left) to balance out the excess product, resulting in more precipitation for a saturated solution.
 Figure 2: The Common-ion effect illustrated. Daniela Lin, Study Smarter Originals.
Figure 2: The Common-ion effect illustrated. Daniela Lin, Study Smarter Originals.
In the graphic above, KCl’s solubility in water is greater than its solubility in an aqueous NaCl solution, as KCl and NaCl contain common ions (Cl).
Common Ion Effect on Solubility of Ionic Salts
After several experiments involving ionic salts, scientists have obtained patterns in data that they have coined as solubility rules.
It’s important for us to be aware of these general trends in order to, later on, calculate the molar solubility of common ions.
Molar solubility is the number of moles of a solute that can be dissolved in a liter of solution until the solution becomes saturated.
For a given temperature, a saturated solution has the maximum amount of solute dissolved into it before precipitation occurs.
Precipitation occurs in a solution when a solid forms, or precipitates out of a solution.
 Figure 3: Solubility table for different salts. The red asterisk indicates exceptions, which are shown in the image below. Daniela Lin, Study Smarter Originals.
Figure 3: Solubility table for different salts. The red asterisk indicates exceptions, which are shown in the image below. Daniela Lin, Study Smarter Originals.
 Figure 4: Exceptions for solubility of ionic salts shown. Daniela Lin, Study Smarter Originals.
Figure 4: Exceptions for solubility of ionic salts shown. Daniela Lin, Study Smarter Originals.
In particular, when an excess of a slightly soluble salt dissolves in water, this creates an equilibrium between the solid salt and salt ions in the saturated solution. Another important thing to know about solubility is the Ksp.
\(K_{sp}\), solubility product constant, is the equilibrium constant for the solubility equilibrium of a slightly soluble salt.
A solute is a substance that dissolves into a solvent.
A
solvent is a substance into which the solute dissolves, resulting in a solution.
At a given temperature, the solubility product constant, \(K_{sp}\) , maintains a constant numerical value even when the concentration of the salt changes. Thus, the higher the \(K_{sp}\) the more soluble the compound is. It isn’t necessary to memorize the solubility tables given above. Instead, familiarize yourself with them and understand that those that form insoluble salts will have lower \(K_{sp}\) ’s and vice-versa for more soluble salts.
This also implies that adding a salt that has a common ion with a given slightly soluble salt (solute) would lead to lower solute solubility and the formation of precipitate sooner than that predicted by the solubility product constant, \(K_{sp}\), for the pure slightly soluble salt in water (solvent) alone. Recall that the \(K_{sp}\) , is calculated for a solute dissolved into a pure solvent.
Molar Solubility and the Common Ion Effect
Now, let's talk about molar solubility and the common ion effect.
We mentioned earlier that molar solubility is the maximum amount of a solute that can dissolve in a pure solvent before the solution becomes saturated.
Solution saturation occurs when added solute forms a precipitate.
A precipitate is the amount of added substance that does not form a solution.
We noted that, once the solution becomes saturated, the solute will no longer dissolve. As mentioned above we usually use the \(K_{sp}\), the product solubility constant, to describe the dissolution of a slightly soluble salt in an aqueous solution. Also, solids are usually not included because their change in concentrations doesn't affect the \(K_{sp}\) since they don't dissolve.
On the other hand, molar solubility describes the dissolution of a substance in a liter of solution. The unit for molar solubility is mol/L or M.
This means that the product solubility constant is not the same thing as the molar solubility.
Consider the equation:
$$X_2Y\left(s \right) \rightarrow X^+\left(aq \right)+Y^-\left(aq \right)$$
where, X2Y (s), stands for a salt of interest, the cation of the salt is, X +, and the anion of the salt is, Y -. Let's say the final concentration of the cation is, [X +] = 0.5 M, then the concentration of the anion would then be, [Y - ] = 0.25 M (because, in this salt, X2Y, there are 2 moles of, X +, for every one mole of, Y - ). As such, the product solubility constant would be given by:
$$K_{sp}=\left[X^+ \right]^2\left[Y^- \right]=\left[0.5 \right]^2\left[0.25 \right]=0.0625$$
While the molar solubility of the hypothetical salt, X2Y, that we added to the solution would have just been, [X2Y] = 0.25 M.
Common Ion Effect Examples
Now that we have read about what \(K_{sp}\) is, how the common ion effect affects the solubility of ionic salts and some general solubility rules, we can move on to studying some common ion effect examples.
What is the concentration of the common ion(s) in the following solution?
A solution containing 0.25 M of each of the following salts: KCl, NaCl, and AgCl.
1. First, we need to identify the common ion in this situation, which is [Cl-]
2.This signifies that [Cl-] = 0.25 M × 3 = 0.75 M, due to the fact that all three salts KCl, NaCl, AgCl contain the common ion, [Cl-]
Answer: Thus, the concentration of the common ion, [Cl-], is 0.75 M.
Keep in mind that if we had something like Magnesium Chloride, MgCl2, it would have contributed 0.25 M × 2 = 0.5 M, for itself alone, since there are 2 Chlorides in it.
Given the following reaction of calcium oxalate dissolving in water:
\(CaC_2O_4 (s) \rightleftharpoons Ca^{2+} (aq) + C_2O_4^{2-} (aq) \)
Generally, what do you think would occur to calcium oxalate \((CaC_2O_4)\) when we add calcium chloride and why?
When calcium chloride dissolves in water we get:
\(CaCl_2 (s) \rightleftharpoons Ca^{2+} (aq) + 2Cl^{-} (aq) \)
According to the Common-ion effect and Le Chatelier's principle the addition of \( CaCl_2\) to the given reaction introduces more
\(Ca^{2+} (aq) \) to the solution due to them sharing a common ion or
\(Ca^{2+} (aq) \) .Adding more \(Ca^{2+} (aq) \) means:
\(CaC_2O_4 (s) \leftarrow Ca^{2+} (aq) + C_2O_4^{2-} (aq) \)
Le Chatelier drives the reaction towards the reactants (left) while the Common-ion effect tells us that there's decreased solubility of calcium oxalate \((CaC_2O_4)\) in the solution that involves calcium chloride \( (CaCl_2)\) .
The common ion, in this case, is the calcium ion. According to the common ion effect, the solubility of the calcium oxalate, CaC2O4, lowers as it precipitates, causing the equilibrium to be disturbed. As such, Le Chatelier will drive the reaction towards the reactants until equilibrium is restored.
What’s the molar solubility of a solution of calcium oxalate, \(CaC_2O_4\) , after we add some calcium chloride, \( (CaCl_2)\), to it?
We note that for calcium oxalate the product solubility constant is:
\(CaC_2O_4 (s) \rightleftharpoons Ca^{2+} (aq) + C_2O_4^{2-} (aq) \)
\(K_{sp}\) = \(2.30\times10^{-9}\)
Let's say we add calcium oxalate to a 0.15 M solution of calcium chloride.
To answer this question we would need to build an ICE or Initial, Change, and Equilibrium chart:
 Figure 5: ICE chart for calcium oxalate with calcium chloride. Daniela Lin, Study Smarter Originals.
Figure 5: ICE chart for calcium oxalate with calcium chloride. Daniela Lin, Study Smarter Originals.
The ICE Chart can be explained as follows:
- Initial, comes from the initial concentration of the calcium cation, Ca2+, that comes from calcium chloride, CaCl2. Recall, that we started with a solution of 0.15 M CaCl2.
- Change, comes from the dissolved ions \( Ca^{2+} \) and \(C_2O_4^{2-} \) (or x) obtained by adding, \(CaC_2O_4\) , to the 0.15M \( (CaCl_2)\) solution.
- Equilibrium, comes from adding the lines Initial and Change together.
Lastly, we setup the \(K_{sp}\) equation:
\(K_{sp}\) = \( [Ca^{2+}] \) \([C_2O_4^{2-}] \)
\(2.30\times10^{-9}\) = (0.15 + x) (x)
This is a quadratic equation that is often inconvenient to solve directly. However, due to calcium oxalate not being very soluble you can consider x as negligible (a very small number) and use the approximation:
\(2.30\times10^{-9}\) = (0.15) (x)
Solving for x we get around \(1.50\times10^{-8}\) M for the molar solubility of calcium oxalate, CaC2O4, in a solution of 0.15M calcium chloride, CaCl.
What about the molar solubility of calcium oxalate, CaC2O4, in pure water?
To answer this question we also need to build an ICE or Initial, Change, and Equilibrium chart:
 Figure 6: ICE Chart for calcium oxalate only. Daniela Lin, Study Smarter Originals.
Figure 6: ICE Chart for calcium oxalate only. Daniela Lin, Study Smarter Originals.
The ICE Chart can be explained as follows:
- Initial, comes from the initial concentrations of each ion. For \( Ca^{2+} \) it's 0 M as we begin with pure water.
- Change, comes from the dissolved ions \( Ca^{2+} \) and \(C_2O_4^{2-} \) (or x) obtained by adding, \(CaC_2O_4\) , to pure water.
- Equilibrium comes from adding the lines Initial and Change together.
Lastly, setup the \(K{sp}\) equation:
\(K_{sp}\) = \( [Ca^{2+}] \) \( [C_2O_4^{2-}] \)
\(2.30\times10^{-9}\) = (x) (x)
Solving for x we get around \(4.80\times10^{-5}\) M for the molar solubility of calcium chloride, CaC2O4, in pure water.
Comparing the two examples, we see that with the addition of a common ion \( Ca^{2+} \) the molar solubility of calcium oxalate, CaC2O4, decreases as precipitation is promoted. This is the common ion effect at work.
You’ve reached the end of this article. We have reviewed the basics of Le Chatelier’s principle and related it to the common ion effect. Furthermore, we have learned about the molar solubility of ions, solubility rules, and gone over some examples to promote more understanding.
For more exercises, please head over to the flashcards!
Common-ion Effect - Key takeaways
Le Chatelier’s principle deals with the disturbance of a chemical reaction equilibrium.
Disturbance involves a change in the system’s conditions such as a change in pressure, temperature, and concentration.
The common ion effect is a shift in equilibrium caused by the addition of an ion that’s already involved in the reaction.
When we add a common ion, the reaction shifts towards the reactants (left) to balance out the excess product, resulting in more precipitation. This means that the common ion effect DECREASES the solubility of ions.
References
- Harwood, William S., F. G. Herring, Jeffry D. Madura, and Ralph H. Petrucci. General Chemistry Principles and Modern Applications. 9th ed. New Jersey: Prentice Hall, 2007.
- Libretexts. (2022, May 8). Common ion effect. Chemistry LibreTexts.
- Solubility and complex-ion equilibria. Solubility. (n.d.).













