When you order boba tea, you are normally asked what level of sweetness you want (low, normal, extra, etc). This is so you have an idea of the sugar content of your drink. Imagine you normally drink low sweetness tea, but, without your knowledge, they give you extra sweetness. You take a sip of your drink expecting a nice, slightly bitter tea, but recoil in disgust as you suck up liquid sugar.
Knowing the composition of species in a mixture is important for chemists too! In this article, we will be diving into the concept of mixtures, and learning how to calculate composition.
- This article is about the composition of mixtures.
- First, we will define a mixture and its two types: homogeneous and heterogeneous.
- Then, we will cover the different separation methods
- Subsequently, we will walk through how to calculate the composition of a mixture
- Lastly, we will explain the concept of gas mixtures and how to calculate partial pressure.
Mixture Definition
Before we discuss the different kinds of mixtures, we should first define what a mixture is.
A mixture is a combination of two or more substances in any proportion. Substances within a mixture keep their original properties and do not undergo a chemical reaction to mix.
We see different kinds of mixtures every day, from salads to saltwater, and even the air we breathe are all mixtures! There are two types of mixtures: homogeneous and heterogeneous. First, we will be explaining homogeneous mixtures.
Homogeneous Mixtures
Homogeneous mixtures are a type of mixture where the composition is uniform.
A great example of a homogeneous mixture is saltwater. When the salt is dissolved, it is dispersed evenly throughout the water. The amount of salt that is dissolved in the water can change, but the distribution is the same.
Here's a diagram to illustrate:
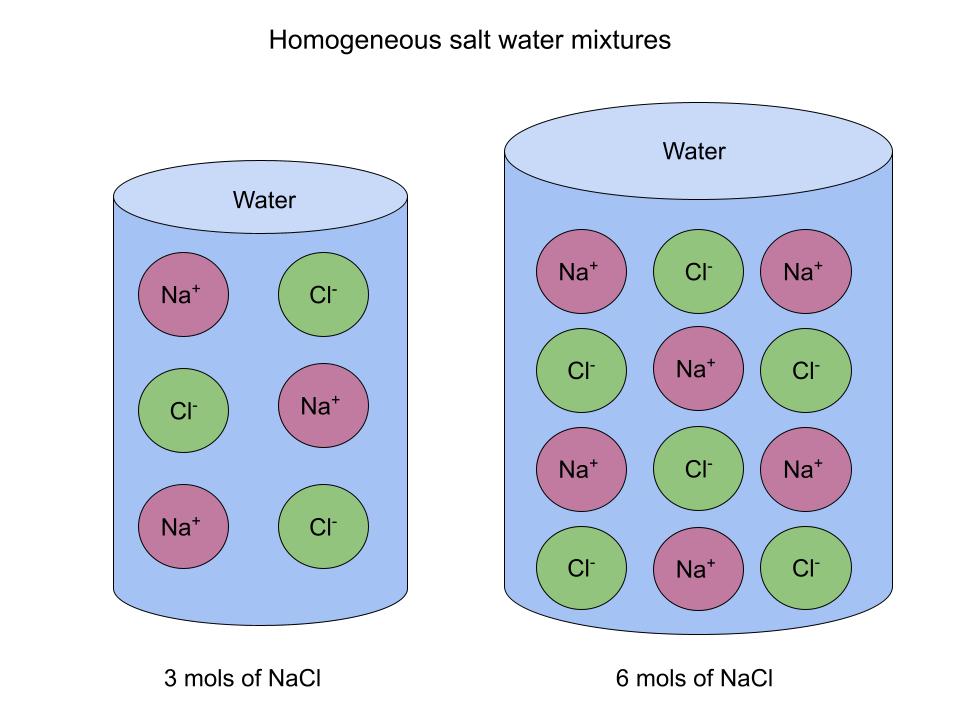
Saltwater is a homogeneous mixture independent of the concentration of salt. StudySmarter Original
Even though each mixture has a different concentration of salt, the distribution is the same. If you cut each sample in half, the composition within each would be the same for both halves.
Heterogeneous mixtures
Now, let's talk about heterogeneous mixtures.
Heterogeneous mixtures are mixtures where the composition is not uniform.
Heterogeneous samples are composed of two or more phases. A great example of a heterogeneous mixture is chocolate chip cookies. The distribution of chocolate chips is essentially random.
A phase is any part of a sample that is uniform. For example, if you mix oil and water, you will have two separate phases: oil and water.
Consider chocolate cookies as an example, the two phases are the cookie and the chocolate chips. The cookie and chocolate chips individually are considered homogeneous since they are uniform in their ingredients (ex. the cookie has an even mixture of flour, egg, sugar, etc.). However, when they are combined, they form a heterogeneous mixture.
Separation of Mixtures
Unlike chemical compounds, mixtures can be separated using non-chemical means. The separation methods rely on the different physical attributes of each component, such as density, boiling point, and size of particles.
There are 4 common ways that chemists use to separate mixtures:
Evaporation
Distillation
Filtration
Separation through a separation funnel
First up, we have evaporation. This technique is typically used to separate a liquid solvent (dissolving substance) and a solid solute (dissolved substance). The solvent is boiled off, and the solute is left behind in its solid state.
Next is distillation. This process focuses on the different volatilities (likelihood to evaporate) of the different liquids in the mixture. Below is what a distillation apparatus looks like:
Distillation experiment. Wikimedia commons.
The mixture is placed in the round-bottom flask and heated. The more volatile liquid will evaporate first, then be condensed and collected as a liquid.
The third method is filtration, which is used to separate an (undissolved) solid from a liquid.
Filtration set up. Wikimedia commons.
A filter paper is placed inside a funnel over a flask. The solid will be caught by the filter paper, and the liquid will pass through it into the flask.
Lastly, we have separation using a separation funnel. This method utilizes the different densities of the liquids in a mixture.
A separation funnel. Wikimedia commons
The liquid mixture is poured into the funnel. The (closed) funnel is shaken and inverted until the liquids have been separated into phases, as you'll see above. The stopcock (handle) is turned to open the funnel to let the lower phase out
Composition of Mixtures: Examples
When looking at a mixture, it's common to want to know its composition. This is especially important in the pharmaceutical industry because we always want to know the percentage of a drug within a pill.
When calculating composition, we are utilizing percent composition.
Let's walk through an example of how to determine the composition of a given substance in a mixture.
You usually drink a coffee that contains 95 mg of caffeine but were gifted an unlabeled bag of coffee. Your friend tells you that it has less caffeine than your usual cup. A serving is 12 g a cup, which is 0.12% nitrogen (N). The molar mass of caffeine (C8H10N4O2) is 194.2 g/mol and the atomic mass of nitrogen is 14.01 g/mol. Is your friend correct?
So our goal here is to see if the caffeine content is lower in the unlabeled coffee than in the coffee you normally drink. We are going to assume that the only source of nitrogen in the coffee is caffeine. We start by multiplying the percentage of nitrogen by the total mass to get the mass of nitrogen.
\(0.12\%*12\,g=0.0144\,g\,N\)
Now we convert from grams of nitrogen to grams of caffeine. We first need to find the moles of nitrogen, so it can be converted to moles of caffeine.
\(\frac{0.0144\,g}{\frac{14.01\,g}{mol}}=0.0010\,mol\,N\)
We see from the chemical formula that there are 4 moles of nitrogen in caffeine (C8H10N4O2), so we need to divide the number of moles of nitrogen by 4 to get the moles of caffeine.
\(0.0010\,mol\,N*\frac{1\,mol\,C_8H_{10}N_4O_2}{4\,mol\,N}=0.00025\,mol\,\text{caffeine}\)
Lastly, we multiply the molar amount by the molar amount to get the concentration of caffeine
\(0.00025\,mol*\frac{194.2\,g}{mol}=0.04855\,g\)
\(0.04855\,g*\frac{1000\,mg}{1\,g}=48.55\,mg\,\text{caffeine}\)
So your friend is correct that there is less caffeine since 48.55<95.
Let's do one more example:
In a container, there is a gaseous mixture of ammonia (NH3) and carbon dioxide (CO2). The percent composition of carbon dioxide is 35%. What is the mass of nitrogen if the total mass of the mixture is 76 g? (The molar mass of ammonia is 17.03 g/mol and the molar mass of nitrogen is 14.01 g/mol).
Our first step is to calculate the percent composition of ammonia since it is the only species with nitrogen in it.
\(100\%-35\%=65\%\,NH_3\)
Next, we multiply the total mass amount by the percent composition of ammonia to get its mass.
\(65\%*76\,g=49.4\,g\,NH_3\)
Now we divide by the molar mass to get the molar amount of ammonia. Since there is one mole (NH3) of nitrogen in ammonia, the molar amounts will be equal.
\(\frac{49.4\,g}{\frac{17.03\,g}{mol}}=2.90\,mol\,NH_3=2.90\,mol\,N\)
Lastly, we multiply the moles of nitrogen by its molar mass to get the mass of nitrogen in the mixture.
\(2.90\,mol*\frac{14.01\,g}{mol}=40.6\,g\,N\)
Gas Mixtures and Partial Pressure
While we calculated the composition of a gas mixture in the previous example, you normally would be measuring gases by their pressure or molar amount. Instead of using percent composition, we use the mole fraction.
The mole fraction (χ) is the ratio of moles of a species to the total moles of a mixture. The formula is: $$\chi_A=\frac{n_A}{n_{tot}}\,\text{where n is the number of moles and}\,n_{tot}\,\text{is the sum of the moles of each species}$$
Partial pressure is the fraction of the total pressure caused by one component.
Here's how we relate these two variables, PV = nRT, using the ideal gas law:
$$\frac{P_{A}}{P_{tot}}=\frac{\frac{n_{A}R}{T}}{\frac{n_{tot}R}{T}}=\frac{n_A}{n_{tot}}=\chi_A$$ Rearranging this we get: $$P_A=\chi_AP_{tot}$$ Now that we have our formulas let's work on a problem.
A 2.5 L container at 365 K contains a 0.52 mol mixture of gas which is 0.17 mol methane (CH4) and 0.35 mol ethane (C2H6). What is the partial pressure of methane and ethane in atm?
First, we need to calculate the total pressure using the ideal gas equation. The ideal gas constant (R) has several values depending on the units. Since we have units of L, K, and atm, we will be using the constant R=0.0821 Latm/molK.
\(P_{tot}V=n_{tot}RT\)
\(P_{tot}V=(0.52\,mol)(0.0821\frac{Latm}{molK})(365\,K)\)
\(P_{tot}(2.5\,L)=15.58\,Latm\)
\(P_{tot}=6.23\,atm\)
Next, we need to calculate χ for both methane and ethane
\(\chi_{CH_4}=\frac{n_{CH_4}}{n_{tot}}\)
\(\chi_{CH_4}=\frac{0.17\,mol}{0.52\,mol}\)
\(\chi_{CH_4}=0.33
\(0.33+\chi_{C_2H_6}=1.00\)
\(\chi_{C_2H_6}=0.67\)
Lastly, we can calculate the partial pressure of each compound
\(P_{CH_4}=P_{tot}\chi_{CH_4}\)
\(P_{CH_4}=6.23\,atm*0.33\)
\(P_{CH_4}=2.06\,atm\)
\(P_{C_2H_6}=P_{tot}\chi_{C_2H_6}\)
\(P_{C_2H_6}=6.23\,atm*0.67\)
\(P_{C_2H_6}=4.17\,atm\)
You can also subtract the partial pressure of methane from the total pressure to get the partial pressure of ethane.
Composition of Mixture - Key takeaways
- A mixture is a combination of two or more substances in any proportion. Substances within a mixture keep their original properties and do not undergo a chemical reaction to mix
- Homogeneous mixtures are a type of mixture where the composition is uniform, while heterogeneous mixtures are mixtures where the composition is not uniform.
- A phase is any part of a sample that is uniform.
- There are 4 common ways that chemists use to separate mixtures:
- Evaporation
- Distillation
- Filtration
- Separation through a separation funnel
- Percent composition is the percentage of an element or compound within a substance.
- The mole fraction (χ) is the ratio of moles of a species to the total moles of a mixture. The formula is: $$\chi_A=\frac{n_A}{n_{tot}}\,\text{where n is the number of moles and}\,n_{tot}\,\text{is the sum of the moles of each species}$$
- Partial pressure is the fraction of the total pressure of a mixture resulting from a species.
Explanations 
Exams 
Magazine 
