Standard Enthalpy of Formation
So, what is the enthalpy of formation? Let's take a look!
Enthalpy, H - the potential energy contained within a chemical bond or chemical interaction when it is released as heat.
Potential Energy - the energy possessed by a molecule by virtue of the positions of its atoms at any given moment.
Chemical bond - the force of attraction that keeps the atoms within a molecule linked together in the appropriate orientation and valence.
Bond Valence - the number of electron pairs within a chemical bond.
The standard enthalpy of formation, ΔHf° - for a given molecule, or compound, is:
...the enthalpy change for the formation of one mole of the substance in its standard state from its elements in their reference form and in their standard states."
Standard State - standard thermodynamic conditions for compounds when listed in a table of thermodynamic data. Typical standard conditions are 1 atmosphere (atm) and 25 °C.
Reference Form - the stablest form of an element under standard conditions.
Stoichiometric Coefficients - the number in front of a chemical species in the balanced equation.
First, let's talk about where the Standard Enthalpy of Formation, ΔHf°, fits into the bigger picture. The overall enthalpy of a chemical reaction (also called the standard enthalpy of reaction, ΔH °) is given by the following equation:
$$\Delta{H^\circ}=\Sigma_{i=1}^n\,[q\Delta{H_f^\circ}(Products)]_i-\Sigma_{i=1}^n\,[r\Delta{H_f^\circ}(Reactants)]_i$$
Where,
Σ, is the summation symbol
q and r are the stoichiometric coefficients of the balanced equation for products and reactants, respectively.
The standard enthalpy of formation of products is ΔHf° (Products)
The standard enthalpy of formation of reactants is, ΔHf° (Reactants)
The summation symbol, Σ, instructs us to add: for example, \(\Sigma_{i=1}^4 a_i=a_1+a_2+a_3+a_4\), means the first term is, a, index, 1, added to term, a, index, 2, added to, a, index, 3, and finally we end with, a, index, 4.
Enthalpy of Formation Equation
As noted earlier, the standard enthalpy of formation terms for products, ΔHf °(Products), and the standard enthalpy of formation terms for reactants, ΔHf °(Reactants), are used to calculate the standard enthalpy of reaction, ΔH °:
$$\Delta{H^\circ}=\Sigma_{i=1}^n\,[q\Delta{H_f^\circ}(Products)]_i-\Sigma_{i=1}^n\,[r\Delta{H_f^\circ}(Reactants)]_i$$
Where, Σ, is the summation symbol and, q, and, r, are the stoichiometric coefficients of the balanced equation for products and reactants, respectively.
For example, consider the following reaction between methane gas, CH4 (g), and chlorine gas, Cl2 (g), to yield carbon tetrachloride liquid, CCl4 (l), and hydrochloric acid gas, HCl (g):
Here we have the following reaction between methane gas, CH4 (g), and chlorine gas, Cl2 (g), to yield carbon tetrachloride liquid, CCl4 (l), and hydrochloric acid gas, HCl (g) :
$$1CH_4\,(g)+4Cl_2\,(g) \rightarrow 1CCl_4\,(l)+4HCl\,(g)$$
Then the enthalpy of formation equation will give the enthalpy of reaction:
\begin{align}\Delta{H^\circ}&=\Sigma_{i=1}^n,[q\Delta{H_f^\circ}(Products)]_i-\Sigma_{i=1}^m\,[r\Delta{H_f^\circ}(Reactants)]_i\\&=[\Delta{H_f^\circ}(CCl_4)+\Delta{H_f^\circ}(HCl)]-[\Delta{H_f^\circ}(CH_4)+\Delta{H_f^\circ}(Cl_2)]\\&=[1\cdot(-139\,kJ/mol)+4\cdot\,(-92.3\,kJ/mol)]-[1\cdot(-74.9\,kJ/mol)+4\cdot(0.0\,kJ/mol)]\\&=-433\,kJ/mol\end{align}
Notice that in the table above, those compounds that are in their elemental state have a standard enthalpy of formation that is equal to zero.
Calculate the Enthalpy of Formation
Now you may ask, "How to calculate the enthalpy of formation?"
1. Let's consider the enthalpy of formation of the product hydrogen chloride, HCl (g), from the reactants, hydrogen gas, H2 (g), and chlorine gas, Cl2 (s), under standard conditions:
$$H_2\,(g)+Cl_2\,(g) \rightarrow HCl\,(g)$$
By referring to the above table of thermodynamic data, we can find the enthalpy of formation of the reactants under standard conditions: 1
Note that the standard enthalpy of formation of elemental hydrogen gas, H2(g), is equal to zero; H2(g): ΔHf° = 0.0 kJ/mol. However, in the present case, the reaction involves breaking the molecular hydrogen bond, which yields atomic hydrogen gas, H (g).
The standard enthalpy of formation of atomic hydrogen gas is H (g): ΔHf° = +218.0 kJ/mol. The same is true for chlorine - the enthalpy of formation of the elemental form of chlorine gas is Cl2 (g): ΔHf° = 0.0 kJ/mol.
Again, in the present case, the reaction involves the breaking of the bonds within the molecular gas, forming atomic chlorine gas; Cl (g): ΔHf° = +121.0 kJ/mol. Then the actual reaction process is given by:
$$H_2\,(g)+Cl_2\,(s) \rightarrow 2H\,(g)+2Cl\,(g) \rightarrow 2HCl\,(g)$$
Notice that we must account for the stoichiometric coefficients of the balanced equation to get the standard enthalpy of formation of reactants, such that:
Standard Enthalpy of the Formation of Reactants:
\begin{align}\Delta{H_f^\circ}(Reactants)&=\Sigma_{i=1}^m\,[r\Delta{H_f^\circ}(Reactants)]_i\\&=2\cdot\Delta{H_f^\circ}(Atomic\,Hydrogen\,gas )+2\cdot\Delta{H_f^\circ}(Atomic\,Chlorine\,gas)]\\&=2\cdot(218.0\,kJ/mol)+2\cdot(121.0\,kJ/mol)\\&=678\,kJ/mol\end{align}
Thus, the standard enthalpy of formation for the production of 2 moles of hydrogen iodide, HCl, is given by:
$$2\cdot \Delta{H_f^\circ}(Hydrogen\,Chloride\,gas)=678\,kJ/mol$$
The enthalpy diagram for this reaction is:
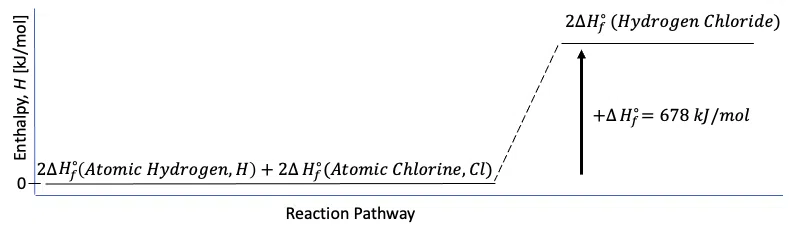
Figure 1: Enthalpy diagram for the enthalpy of formation of hydrogen chloride, HCl.
Thus, the synthesis of hydrogen chloride from elemental hydrogen and chlorine is an energy-absorbing, or endothermic, reaction.
Now we may ask, "How to calculate the enthalpy of formation using Hess's law?"
Hess's Law - also known as Hess's Law of Constant Heat Summation, states that during all the steps of any chemical reaction the total enthalpy change, ΔH, does not depend on the order in which the steps, from reactants to intermediates to products, are taken but only depends on the sum of the enthalpies of all of the reactions in any order.
Let's consider again the following reaction between methane gas (CH4 (g)) and chlorine gas (Cl2 (g)) to yield carbon tetrachloride liquid (CCl4 (l)) and hydrochloric acid gas (HCl (g)):
$$1CH_4\,(g)+4Cl_2\,(g) \rightarrow 1CCl_4\,(g)+4HCl\,(g)$$
From the table for Standard Enthalpies of Formation 1 (at 25°C), above, we pick out the enthalpies of formation for CH4 (g), Cl2 (g), and HCl (g). Then we can write the thermochemical equations in the following way:
\begin{align}C\,(Graphite)+2\,H_2\,(g) \rightarrow CH_4\,(g):\,\Delta{H_f^\circ}&=-74.9\,kJ/mol\,\,\,\,\,\,\,(1)\\C\,(Graphite)+Cl_2\,(g) \rightarrow CCl_4\,(l):\,\Delta{H_f^\circ}&=-139\,kJ/mol\,\,\,\,\,\,\,\,\,(2)\\\frac{1}{2}H_2+\frac{1}{2}Cl_2\,(g) \rightarrow HCl\,(g):\,\Delta{H_f^\circ}&=-92.3\,kJ/mol\,\,\,\,\,\,\,\,(3)\end{align}
Applying Hess's Law, our aim is to isolate CH4 (g) on the left-hand side while isolating carbon tetrachloride, CCl4, and 4HCl (g), on the right-hand side. Additionally, we want to eliminate all elements in their reference form, because these are equal to 0.0 kJ/mol and do not contribute to the heat summation. So what we do is reverse equation (1) (above), add equation (2) and multiply equation (3) by the number four. Thus:
\begin{align}CH_4\,(g) \rightarrow C\,(Graphite)+2\,H_2\,(g)&\,\,\,\,\,\,\,\,\,\,\,\,\,1\cdot (+74.9\,kJ/mol)\\C\,(Graphite)+Cl_2\,(g) \rightarrow CCl_4\,(l)&\,\,\,\,\,\,\,\,+1\cdot (-139\,kJ/mol)\\\underline{2H_2\,(g)+2Cl_2\,(g) \rightarrow 4HCl\,(g)}&\,\,\,\,\,\,\,\,\underline{+4\cdot (-92.3\,kJ/mol)}\\CH_4\,(g)+4Cl_2\,(g) \rightarrow CCl_4\,(l)+4HCl\,(g)&\,\,\,\,\,\,\,\Delta{H^\circ}=-433.3\,kJ/mol\end{align}
Enthalpy of Formation of Water
Let's consider the standard entahlpy of formation of water, H2O (l), from hydrogen gas, H2, and oxygen gas, O2. The reaction is then:
$$2H_2\,(g)+O_2\,(g) \rightarrow 2H_2O\,(l):\,\Delta{H_f^\circ}=-571.6\,kJ/mol$$
Now, to write this for a reaction that produces 1 mole of water, we multiply this equation by a factor of 1/2:
$$\frac{1}{2}\cdot 2H_2\,(g)+\frac{1}{2}\cdot O_2\,(g) \rightarrow \frac{1}{2}\cdot2H_2O\,(l):\,\Delta{H_f^\circ}=\frac{1}{2}\cdot(-571.6\,kJ/mol)=-285.8kJ/mol$$
This is then the standard enthalpy of formation for 1 mole of liquid water.
Now we might ask, "What best describes the enthalpy of formation of a substance?"
In all cases, the enthalpy of formation of a substance is associated with the potential energy that is released, as heat, from the breaking of a chemical bond within a compound.
Enthalpy of Formation - Key takeaways
- Enthalpy is the potential energy contained within a chemical bond or chemical interaction when it is released as heat.
- The overall enthalpy of a chemical reaction (also called the standard enthalpy of reaction, ΔH °) is given by the following equation:
$$\Delta{H^\circ}=\Sigma_{i=1}^n\,[q\Delta{H_f^\circ}(Products)]_i-\Sigma_{i=1}^n\,[r\Delta{H_f^\circ}(Reactants)]_i$$
Where, Σ, is the summation symbol and, q, and, r, are the stoichiometric coefficients of the balanced equation for products and reactants, respectively. The standard enthalpy of formation of products is, ΔHf° (Products), while the standard enthalpy of formation of reactants is, ΔHf° (Reactants).
- Standard enthalpy of formation is "...the enthalpy change for the formation of one mole of the substance in its standard state from its elements in their reference form and in their standard states." 1
- Hess's Law, also known as Hess's Law of Constant Heat Summation, states that during all the steps of any chemical reaction the total enthalpy change, ΔH, does not depend on the order in which the steps, from reactants to intermediates to products, are taken but only depends on the sum of the enthalpies of all of the reactions in any order.
References
- General Chemistry, Darrell D. Ebbing, 4th ed.








