Have you ever sprayed an air freshener in a room? At first, you can only smell it directly where you sprayed, but eventually, the particles will spread across the room and can be smelt anywhere.
Now, what would happen if you sprayed two different air fresheners at the same time in the same general place? While the scents will be mixed, one will be smelt on the opposite end of the room earlier than the other. Why is this? Well, Graham's law has the answer, continue reading to find out!
- This article covers Graham's law.
- First, we will define Graham's law.
- Next, we will look at Graham's law equation.
- Then we will look at the two parts of Graham's law: Graham's law of diffusion and Graham's law of effusion.
- Lastly, we will work on some examples using Graham's law.
Graham's Law Definition
Let's start by looking at the definition of Graham's law.
Graham's law states that the rate of diffusion or effusion of a gas is inversely proportional to the square root of the molar masses of its particles.
Diffusion is the process of particles moving from an area of high density to one of low density
Effusion is the process of gas particles escaping their container into another container through a small hole. This hole's diameter is much smaller than the particle's mean free path, which is the distance a particle travels before it collides with something. Essentially, this means that only one particle can travel through the hole at a time.
Now, this is a bit of a tricky definition. To help us out, we are first going to look at the equation.
Graham's Law Equation
The equation for graham's law is:$$\frac{Rate_A}{Rate_B}=\sqrt{\frac{M_B}{M_A}}$$
Where,
- MA and RateA are the molar mass and rate of effusion/diffusion of gas, A respectively.
- MB and RateB are the respective molar mass and rate of effusion/diffusion of gas, B.
What this basically tells us is the ratio of rates based on their masses. In simpler terms, the heavier the gas, the slower it's going to go. Here's an example:
Calculate the rate of effusion/diffusion for a container of both helium (He) and neon (Ne) gas.
The molar mass of helium is 4.00 g/mol, and the molar mass of neon is 20.2 g/mol. Plugging this in, we get:
$$\frac{Rate_A}{Rate_B}=\sqrt{\frac{M_B}{M_A}}$$
$$\frac{Rate_{He}}{Rate_{Ne}}=\sqrt{\frac{M_{Ne}}{M_{He}}}$$
$$\frac{Rate_{He}}{Rate_{Ne}}=\sqrt{\frac{20.2\frac{g}{mol}}{4.00\frac{g}{mol}}}$$
$$\frac{Rate_{He}}{Rate_{Ne}}=\sqrt{5.05}$$
$$\frac{Rate_{He}}{Rate_{Ne}} =2.25$$
This means that helium will effuse/diffuse 2.25x times faster than neon
To better understand this concept, let's split this law up into two parts: diffusion and effusion.
Graham's Law of Diffusion
Let's first talk a bit more about what diffusion is. Like we talked about in the introduction when you spray an air freshener the spray will only be smelt in the direct area, but the particles will eventually spread across the room.
Here's a diagram of what's happening:
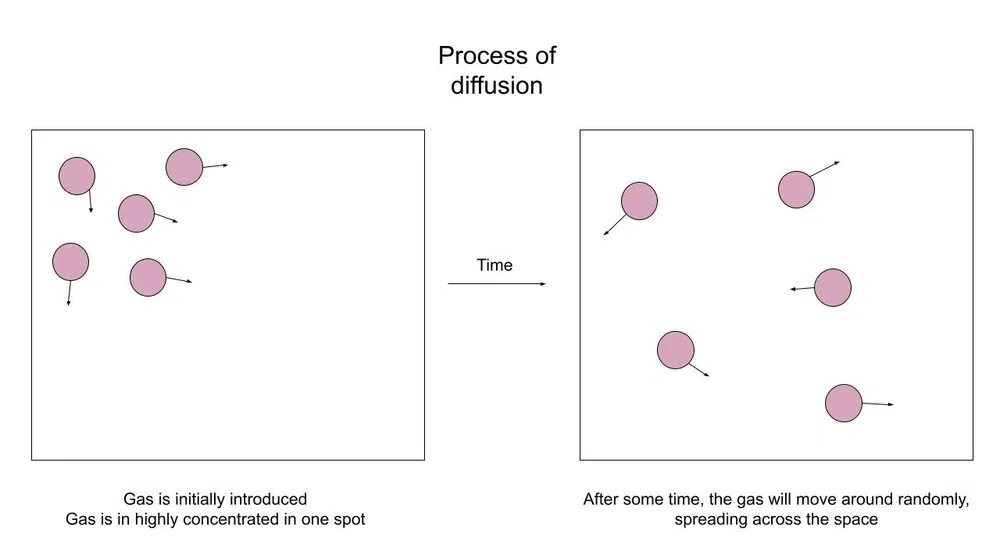
Fig.1-Particles diffuse across a space
The purpose of diffusion is to create an equilibrium. Equilibrium is essentially a state of balance. In this case, equilibrium means a balanced concentration across the whole container.
So, what happens when there are two gases? That's where Graham's law steps come in.
Our main assumption is that both gases are at the same temperature, and therefore have the same kinetic energy, which is the energy of motion.
In fact, that's where graham's law comes from. Here's the formula for kinetic energy:
$$KE=\frac{1}{2}*M_A*\nu_{rms}^2$$
Where KE is kinetic energy, MA is the molar mass of species A, and νrms is the root-mean-square speed.
Root-mean-square speed (RMS speed) is the average speed of a gas. The formula is:
$$\nu_{rms}=\sqrt{3RTM}$$
Where R is the ideal gas constant, T is the temperature, and M is the molar mass of the gas.
You don't really need to worry about the exact definition of RMS speed, so you can just think of it as "speed" for now.
For gases, we don't use normal velocity since the net velocity of a gas is zero, since the gases will move in all directions (i.e. they will cancel each other out since velocity is speed + direction)
Continuing on with our derivation, we are going to set the kinetic energies of our two gases (A and B) equal to each other:
$$KE=\frac{1}{2}*M_A*\nu_{rms,A}^2=\frac{1}{2}*M_B*\nu_{rms,B}^2$$
Next, we can cancel out the 1/2, since it is on both sides:
$$M_A*\nu_{rms,A}^2=M_B*\nu{rms,B}^2$$
Then, we move both of our molar mass terms onto one side and our RMS speed terms onto the other:
$$\frac{M_A}{M_B}=\frac{\nu_rms,B^2}{\nu_rms,A^2}$$
Lastly, we take the square root of both sides:
$$\sqrt\frac{M_A}{M_B}=\frac{\nu_rms,B}{\nu_rms,A}$$
Now that we know how we got our equation, let's see it in action.Earlier, we calculated that helium would diffuse 2.25x faster than neon, below is a diagram showing this process:
Fig.2-Graham's law of diffusion experiment.
Essentially, helium is going to diffuse faster since it is lighter. This means that more helium particles will reach the neon "side".
Think of it like rolling a ping-pong ball versus a soccer ball. If I rolled both balls with the exact same amount of energy, the ping-pong ball will travel farther (i.e. have a greater velocity) than the soccer ball since the ping-pong ball is much lighter.
However, after a certain amount of time, there will be an equilibrium of gases, i.e. the same concentration on both sides.
Graham's law of effusion
Now let's talk about effusion.
As a reminder, here's the definition of effusion from earlier:
Effusion is the process of gas particles escaping their container into another container through a small hole. This hole's diameter is much smaller than the particle's mean free path, which is the distance a particle travels before it collides with something. Essentially, this means that only one particle can travel through the hole at a time.
Essentially, effusion is the same as diffusion, except the particles are passing through a hole instead of moving through an open space.Here's what this process looks like:
Fig.3 Gas effusion
Like with diffusion, during effusion, gases are moving to a less concentrated area. Now let's see what effusion looks like with two gases according to Graham's law:
Fig.4-Graham's law of effusion for helium and neon
The two balloons are connected by a small hole, which we assumed to be sealed (i.e. no gas can escape besides the exchange between the two balloons). Since the helium moves faster, it will effuse at a faster rate than the neon. This means the neon balloon will inflate as the helium effuses in, while the helium balloon deflates since it is losing that helium.
Graham's Law Examples
Now that we better understand the concept of effusion and diffusion, let's work on some examples!
A sample of Nitrogen and oxygen gas is in a container with a small hole leading to another, empty container. Which of the gases will effuse first?
- The molar mass of Nitrogen is 14.00 g/mol and the molar mass of oxygen is 16.00 g/mol.
While we can plug this into our equation, all we really need to do is look at the molar masses. Nitrogen is lighter, so it will effuse faster, and therefore first.
Now let's do an example where we actually calculate something:
What is the ratio of the rate of diffusion for chlorine (Cl2) gas and krypton (Kr) gas?
- The molar mass of chlorine is 35.45 g/mol and the molar mass of krypton is 83.80 g/mol.
Since chlorine gas is Cl2 and not Cl, we need to double the molar mass value when we plug it into our equation:
$$\frac{Rate_A}{Rate_B}=\sqrt{\frac{M_B}{M_A}}$$
$$\frac{Rate_{Cl2}}{Rate_{Kr}}=\sqrt{\frac{M_{Kr}}{M_{Cl2}}}$$
$$\frac{Rate_{Cl2}}{Rate_{Kr}}=\sqrt{\frac{83.80\frac{g}{mol}}{(35.45\frac{g}{mol}*2)}}$$
$$\frac{Rate_{Cl2}}{Rate_{Kr}}=\sqrt{\frac{83.80\frac{g}{mol}}{70.9\frac{g}{mol}}}$$
$$\frac{Rate_{Cl2}}{Rate_{Kr}}=\sqrt{1.18}$$
$$\frac{Rate_{Cl2}}{Rate_{Kr}}=1.09$$
Since chlorine gas and krypton gas are similar in mass, the difference in the rate of diffusion isn't that large. The greater the difference in mass, the greater the ratio of rates will be.
Graham's Law - Key takeaways
Explanations 
Exams 
Magazine 
