Our bodies are well-oiled machines. They have a series of "fail-safes" to keep our body going when something goes wrong. Our body uses compounds called buffers to prevent different bodily systems from getting too acidic or basic.
One example of this is in our blood. There is a solution of carbonic acid and bicarbonate anion that keep our body at a pH between 7.35 and 7.45. Having a pH as low as 6.8 or as high as 7.8 can lead to death!
In this article, we will be learning about the Henderson-Hasselbalch equation and how it relates to buffers. We will see how buffers keep pH stable, so our bodies can keep chugging!
- This article covers the Henderson-Hasselbalch equation.
- First, we will do a brief refresher on weak acid, weak bases, and buffers.
- Then, we will look at what the Henderson-Hasselbalch equation is and see how it was derived.
- Then, we will learn how to use the equation to calculate the pH of a buffer solution.
- Lastly, we will learn how to calculate the pH of a buffer system when a strong acid and strong base are added.
Background Info: Weak acids, Weak bases, and Buffers
Before we look at an equation, we should first brush up on the concept of weak acids and bases, according to the Bronsted-Lowry definition of acids and bases.
Acids are species that donate a proton (H+ ion), while bases are species that receive a proton.
Here is what a simple acid-base reaction looks like:
$$HA + B^- \rightarrow A^- + HB$$
Here, "B" refers to the base. When it becomes HB, it is the conjugate acid, meaning it can now act as an acid. "HA" is our acid, and A- is the conjugate base.
For example, here is reaction between hydrochloric acid (HCl) and a hydroxide ion (OH-):
$$HCl + OH^- \rightarrow Cl^- + H_2O$$
The chlorine ion is the conjugate base, since it wants to regain that hydrogen. Water is the conjugate acid, since it can lose a hydrogen to reform hydroxide.
In this example, the reverse reaction will not occur. HCl is a strong acid, meaning it dissociates 100% in water. Strong acids will form very weak conjugate bases, so the chloride ion will not take the proton back from water.
Water is amphiprotic, meaning it can act as an acid or base depending on the circumstances.
There are weak and strong acids/bases. We often use the acid or base dissociation constant to determine the strength of an acid or base.
The acid dissociation constant (Ka) measures how strong an acid is.
For an example reaction:
$$HA \rightleftharpoons A^- + H^+$$
The Ka is:
$$K_a=\frac{[A^-][H^+]}{[HA]}$$
The smaller the Ka is, the weaker the acid
For example, the dissociation constant for HCl would be:
$$HCl \rightleftharpoons Cl^- + H^+$$
$$K_a=\frac{[Cl^-][H^+]}{[HCl]}$$
The base dissociation constant (Kb) is the exact same concept, except it measures the strength of bases.
For a general reaction:
$$B + H_2O \rightleftharpoons HB^+ + OH^-$$
$$K_b=\frac{[HB^+][OH^-]}{[B]}$$
Only aqueous (dissolved in water) species are applied to the formula. Since water is a liquid, it is not added.
As an example, here is the Kb for ammonia (NH3):
$$NH_3 + H_2O \rightleftharpoons NH_4^+ + OH^-$$
$$K_b=\frac{[NH_4^+][OH^-]}{[NH_3]}$$
Weak acid/bases don't dissociate completely. This means that there is a large concentration of our acid/base left when it dissociates. Here is what that looks like:
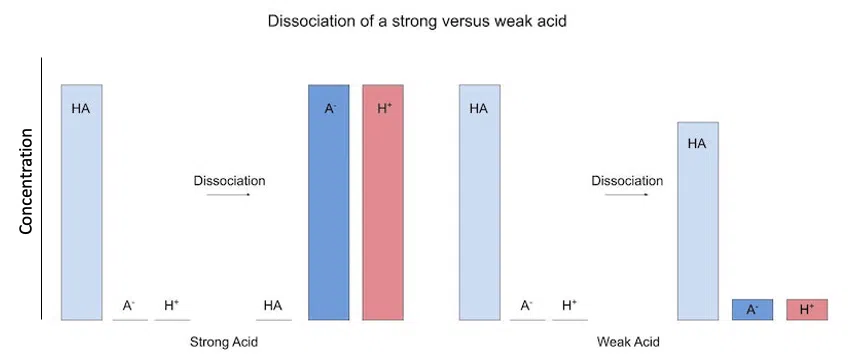
Fig. 1 - Dissociation of strong versus weak acids
Here, our vertical axis is concentration, so the taller the bar, the greater the concentration.
As you can see, there is a lot of acid left when it partially dissociates. This property is why weak acids/bases are important as buffers.
A buffer is a solution composed of a weak acid/base and its conjugate. This solution is designed to keep the pH of a system stable when a small volume of strong/acid base is added.
pH is a logarithmic scale that measures the acidity/alkalinity of a solution. It ranges from 0 to 14, with 0 being very acidic and 14 being very basic.
More specifically, it's formula is: $$pH=-log[H^+]$$
Where [H+] is the concentration of hydrogen cations (protons).
When an acid is added to a system, the concentration of hydrogen ([H+]) increases, which leads to a decrease in the pH (since it is a negative logarithmic scale). When a base is added to a system, it will take up protons present in the system, which increases the pH.
Buffers are designed to prevent the addition or subtraction of pH. They neutralize any added acid/base up to a certain point (called the buffer capacity). Buffer effectiveness is measured by how stable it keeps the pH.
This is where the Henderson-Hasselbalch equation comes in.
The Henderson-Hasselbalch equation measures the change in pH of a buffer system when a strong acid or base is added.
A buffer's capacity has to do with the molar amounts. As long as the strong acid/base being added to the buffer solution is less than the acid/base in the buffer, the buffer will be effective. If the species being added exceeds that of the buffer, then the buffer can't neutralize it, and the pH will change drastically.
pH equation Henderson-Hasselbalch
The formula for the Henderson-Hasselbalch equation is as follows:
$$\text{p}\text{H}=pK_a+log(\frac{[A^-]}{[HA]})$$
Where,
pKa is the negative logarithm of the acid dissociation constant.
[A-] is the concentration of the weak/conjugate base.
[HA] is the concentration of the weak/conjugate acid.
Henderson-Hasselbalch Equation Derivation
So, where does this equation come from anyway? Well, let's look back at our simple acid dissociation:
$$HA \rightleftharpoons H^+ + A^-$$
If set up the acid dissociation constant equation, it looks like this:
$$K_a=\frac{[H^+][A^-]}{[HA]}$$
Next, we take the negative logarithm, so we have the pKa:
$$pK_a=-log(\frac{[H^+][A^-]}{[HA]})$$
Now we are going to use one of the rules of logarithms to expand this equation:
$$-log({x}{y})=-log(x)-log(y)$$
Here, "x" is [HA] while "y" is \(\frac{[A^-]}{[HA]}\). This is because we want the, \(-log{([H^+])}\), term left alone, which you will see why in just a moment:
$$pK_a=-log([H^+])-log(\frac{[A^-]}{[HA]}))$$
The reason we did this is that, \(p\,H=-log{([H^+])}\), is the formal definition of pH. pH actually stands for "potential hydrogen". So using this definition, we end up with:
$$pK_a=pH-log(\frac{[A^-]}{[HA]})$$
Lastly, we add the logarithm portion to the other side so that we end up solving for pH:
$$pH=pK_a+log(\frac{[A^-]}{[HA]})$$
When we derived the formula, we used a general acid dissociation. However, this derivation still works with any acid, which is why we can use this equation for any buffer system.
Let's look at an example!
Derive the Henderson-Hasselbalch equation using the dissociation of the weak acid hydrofluoric acid (HF).
First, we write the reaction:
$$HF \rightleftharpoons F^- + H^+$$
Then, we set up the dissociation constant:
$$K_a=\frac{[F^-][H^+]}{[HF]}$$
Next, we take the negative log to get the pKa:
$$-log\,(K_a)=pK_a=-log(\frac{[F^-][H^+]}{[HF]})$$
or just,
$$pK_a=-log(\frac{[F^-][H^+]}{[HF]})$$
Then we expand logarithm on the left-hand side, like before:
$$-log({x}{y})=-log(x)-log(y)$$
Here, "x" is [H+] while "y" is \(\frac{[F^-]}{[HF]}\).
$$pK_a=-log([H^+])-log(\frac{[F^-]}{[HF]})$$
and making sure to substitute in pH:
$$pK_a=pH-log(\frac{[F^-]}{[HF]}$$
Lastly, we add our logarithm term to the other side, so we are solving for pH instead of pKa:
$$pH=pK_a+log(\frac{[F^-]}{[HF]}$$
Henderson-Hasselbalch Equation Examples
We use the Henderson-Hasselbalch in three different scenarios:
To find the pH of a buffer solution without any additives.
To find the pH of the solution when a strong acid is added.
To find the pH of the solution when a strong base is added.
We are going to walk through an example of each, so let's start by calculating the pH of just the buffer solution:
A buffer solution is made of 0.20 M HF and 0.15 M NaF. What is the pH of the solution if the pKa of HF is 3.17?
Since nothing is being added to the system, we just need to plug in our variables once we have identified our acid and base. HF is our acid, so it goes in the denominator, while NaF (or F-, Na+ is just used for charge balancing) is the base, so it goes in the numerator.
$$pH=pK_a+log(\frac{[A^-]}{[HA]})$$
$$pH=pK_a+log(\frac{[F^-]}{[HF]}$$
$$pH=3.17+log(\frac{0.15\,M}{0.20\,M})$$
$$pH=3.17-0.125$$
$$pH=3.05$$
Henderson-Hasselbalch Estimation
It's important to remember that this equation is an estimation tool. In reality, some weak acid will dissociate into its components (i.e. hydrogen and the weak base), which would alter the pH. This equation assumes that this change is minimal.
Here's how we would solve the above equation using an ICE (Initial Change Equilibrium) table. We are going to treat F- the same as NaF since the Na+ is mainly there for charge balance.
$$HF \rightleftharpoons H^+ + F^-$$
| Species | HF | H+ | F- |
| Initial | 0.20 M | ~0 | 0.15 M |
| Change | -x | +x | +x |
| Equilibrium | 0.20-x | x | 0.15+x |
We can plug these values into the expression for Ka and solve for x.
$$ pKa=-log[K_a] $$
$$ 3.17=-log[K_a] $$
$$ 10^{-3.17}=K_a] $$
$$ K_a=6.761x10^{-4} $$
$$ K_a = \frac{[H^+][F^-]} {[HF]} $$
$$ 6.761x10^{-4}= \frac{[x][0.15+x]} {0.20-x]} $$
$$ 6.76x10^{-4} =\frac{0.15x+x^2}{0.20-x} $$
$$ 1.352x10^{-4} - 6.761x10^{-4} x= 0.15x+x^2 $$
$$ x^2 + 0.15068x -1.352x10^{-4} =0 $$
Using the quadratic formula, we get x = 8.912x10-4 (the negative value isn't used since you can't have a negative concentration).
Lastly, we plug this into the definition for pH
$$pH=-log[H^+] $$
$$pH=-log(8.912x10^{-4} ) $$
$$pH=3.05$$
Since the effect of the acid dissociation was small, this pH is the same as what we calculated earlier, which shows why we use this estimation instead of all that math!
Henderson Hasselbalch Equation for Strong Acids
Now that we know how to calculate the general pH, now let's work on calculating the pH when a strong acid is added.
0.1 L of 0.6 M HCl is added to a 1.1 L buffer solution of 0.32 mol CH3COOH and 0.35 mol CH3COONa. This brings the total volume to 1.2 L. If the pKa of acetic acid (CH3COOH) is 4.76, what is the pH of the solution?
$$CH_3COOH \rightleftharpoons CH_3COO^- + H^+$$
Here, our acid is acetic acid (CH3COOH), our weak base is the acetate anion (CH3COO-), while our strong acid is H+. Note that one of the sources of H+ strong acid is from, HCl, which completely ionizies to H+ and Cl- because it is a strong acid.
Our first step is to determine the weak base concentration. The total volume is 1.2 L, so all we need to do is divide the moles of sodium acetate (CH3COONa) by the volume to get the concentration:
$$\frac{0.35\,mol}{1.2\,L}=0.29\,M=[A^-]$$
Our next step is to find the concentration of acid. When we look at the [HA] term, that refers to the concentration of all acid, not just the weak acid.
First, we need to get the moles of HCl by multiplying the concentration by the volume added:
$$0.6\,\frac{mol}{L}*0.1\,L=0.06\,mol\,HCl$$
Now we can get the acid concentration by adding the moles of HCl and acetic acid and dividing that by the total concentration:
$$0.06\,mol\,HCl+0.32\,mol\,CH_3COOH=0.38\,mol\,HA$$
$$\frac{0.38\,mol}{1.2\,L}=0.32\,M\,HA$$
Now we can plug in our variables and solve for pH:
$$pH=pK_a+log(\frac{[A^-]}{[HA]})$$
$$pH=4.76+log(\frac{0.29\,M}{0.32\,M})$$
$$pH=4.76-0.04$$
$$pH=4.72$$
Henderson Hasselbalch Equation for Strong Bases
When a strong base is added, we follow the same steps as before, except we need to calculate the total base concentration, not the acid concentration.
A 0.15 L sample of 0.5 M NaOH was added to a 1.6 L buffer solution containing 0.17 mol HN3 (hydrazoic acid) and 0.12 mol NaN3 (sodium azide). If the pKa of hydrazoic acid is 4.7, what is the change in pH when the base is added?
Since we want to know the change in pH, we also need to calculate the pH of just the buffer solution. We don't need to solve for concentration here, since the volume variable cancels out.
$$For\,the\,buffer\,solution: HN_3 \rightleftharpoons N_3^-+H^+$$
Here, our weak acid is hydrazoic acid (HN3), our weak base is the azide anion, (N3-), while our strong base is OH-. Note that one of the sources of OH- strong base is from NaOH, which completely ionizies to Na+ and OH-, because it is a strong base.
Continuing with our calculation of the pH of the buffer:
$$pH=pK_a+log(\frac{[A^-]}{[HA]})$$
$$pH=4.7+log(\frac{0.12\,mol}{0.17\,mol})$$
$$pH=4.7-0.15$$
$$pH=4.55$$
Now we can start on the second portion of this problem.
First, we calculate the concentration of acid. Since we are adding 0.15 L of the strong base, OH-, to a 1.6 L buffer solution, our new total volume is 1.85 L.
$$[HA]=\frac{0.17\,mol}{1.85\,L}=0.092\,M$$
Next, we need the molar amount of NaOH, then we can solve for the concentration of base:
$$0.5\,\frac{mol}{L}*0.15\,L=0.075\,mol$$
$$0.075\,mol\,NaOH+0.12\,mol\,NaN_3=0.195\,mol$$
$$\frac{0.195\,mol}{1.85\,L}=0.105\,M=[A^-]$$
Now we can plug this into our formula
$$pH=pK_a+log(\frac{[A^-]}{[HA]})$$
$$pH=4.7+log(\frac{0.105\,M}{0.092\,M})$$
$$pH=4.7+0.057$$
$$pH=4.757$$
Our last step is to subtract the old pH from the new pH to get the pH change:
$$\Delta pH=pH_{final}-pH_{initial}$$
$$\Delta pH=4.757-4.55$$
$$\Delta pH=0.207$$
Now, I hope that you feel more confident in your understanding of the Henderson-Hasselbalch Equation!
Henderson-Hasselbalch Equation - Key takeaways
- A buffer is a solution composed of a weak acid/base and its conjugate. This solution is designed to keep the pH of a system stable when a small volume of strong/acid base is added.
- pH measure how acidic/basic a species is. It ranges from 0 to 14, with 0 being very acidic and 14 being very basic.
- The Henderson-Hasselbalch equation measures the change in pH of a buffer system when a strong acid or base is added.
- The formula for the Henderson-Hasselbalch equation is: $$pH=pK_a+log(\frac{[A^-]}{[HA]})$$
- When a strong acid or base is added to a buffer solution...:
- Acid: Add the concentration of the strong acid to the concentration of the weak acid to get the total acid concentration([HA])
- Base: Add the concentration of the strong base to the concentration of the weak base to get the total base concentration ([A-])
Explanations 
Exams 
Magazine 
