Americas
Europe
Imagine you have 2 strong magnets, due to their attraction it's hard to pull them apart. If you add paper between them, it gets easier to pull them apart. Now imagine adding 20 pages of paper between them. Well, now it's way much easier to pull them apart. This is because the paper is shielding the magnets from each other. As for the shielding effect in chemistry, electrons are shielded from the positive charge of the nucleus.
Explore our app and discover over 50 million learning materials for free.
Lerne mit deinen Freunden und bleibe auf dem richtigen Kurs mit deinen persönlichen Lernstatistiken
Jetzt kostenlos anmeldenImagine you have 2 strong magnets, due to their attraction it's hard to pull them apart. If you add paper between them, it gets easier to pull them apart. Now imagine adding 20 pages of paper between them. Well, now it's way much easier to pull them apart. This is because the paper is shielding the magnets from each other. As for the shielding effect in chemistry, electrons are shielded from the positive charge of the nucleus.
Each level of electrons acts as another sheet of paper that blocks some charge from reaching the electron we are looking at. In this article, we will look at how the shielding effect works and how it affects the electrons involved.
Let's start by looking at the definition of shielding effect.
The shielding effect describes how electrons closer to the nucleus "shield" the electrons farther away from the positive charge of the nucleus.
So, what do we mean by "shielding" exactly? Here's a basic diagram of an atom:
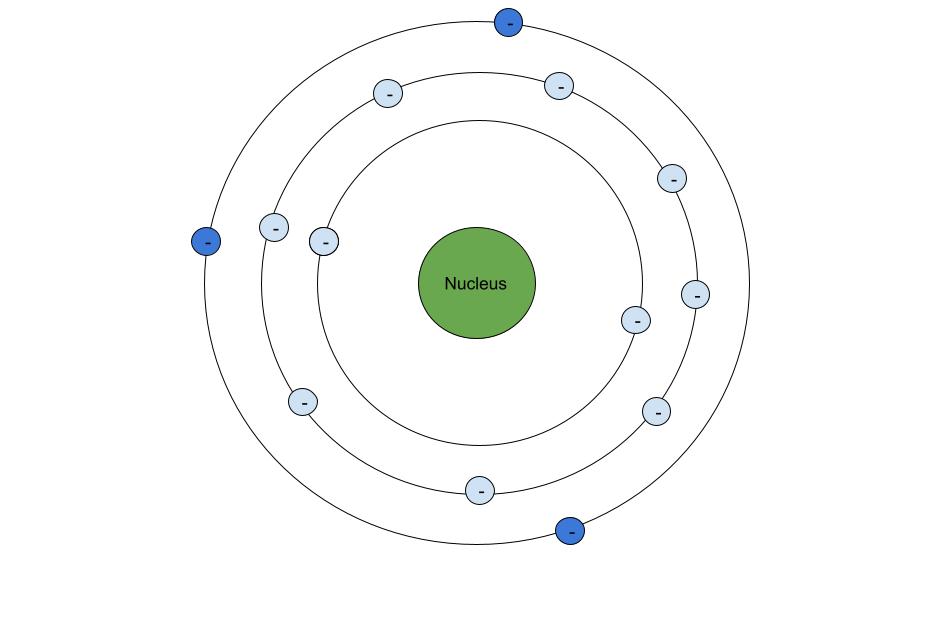
The core electrons (light blue) shield the Valence Electrons (dark blue) from some of the nucleus's charge. StudySmarter Original
The different rings represent different energy levels. The electrons in light blue are the core electrons, these are all the electrons not in the outer shell. The electrons in dark blue are the Valence Electrons, which are the electrons in the outer shell, these are also the electrons that participate in bonding.
Electrons are going to repel other electrons, so as these electrons are orbiting around the nucleus, they will feel a slight "push". However, they are still being "pulled" by the nucleus. The "pushing" of the core electrons negates some "pulling" done by the nucleus, similar to tug-of-war.
The way we represent shielding is by using the shielding effect formula for Zeff.
Zeff (Effective nuclear charge) is the charge an electron "feels" when it is being shielded. The equation for this is:
$$Z_{eff}=Z-S$$
Where Z is the number of protons and S is the number of core electrons (or electrons between electron and nucleus).
So, Zeff, is the net "pull" our electron feels. Normally, we only care about the, Zeff, of valence electrons, but electrons in lower energy levels still experience the shielding effect. Let's look at an example:
Calculate the Zeff for a valence electron in fluorine.
Fluorine's atomic number is 9, so it has 9 protons. When we fill our electrons shells, the first holds 2 electrons, while each one after that holds 8. So for fluorine, there are only 2 core electrons and 7 valence electrons.$$\begin {align}Z_{eff}&=Z-S \\Z_{eff}&=9-2 \\Z_{eff}&=7\end {align} $$
So, now we know that the Zeff for a valence electron in fluorine is 7, so what does that mean exactly? To better understand this, let's look at another example:
Calculate the Zeff of a valence electron in beryllium.
Beryllium's atomic number is 4, so it has 4 protons. It also has 2 core electrons.$$\begin {align}Z_{eff}&=Z-S \\Z_{eff}&=4-2 \\Z_{eff}&=2\end {align}$$
So, the Zeff of beryllium is 2, and it's 7 for fluorine. This ties into their charge and how they bond. The charge on the most common ion of beryllium, the beryllium cation is +2, meaning it can lose 2 electrons. However, the charge on the most common ion of fluorine, the fluoride anion has a charge of -1, so it wants to gain 1 electron to fill its octet (the outermost shell can hold 8 electrons).
Fluorine's nucleus has a greater pull on its valence electrons, so those electrons want to stay where they are and gain an electron, whereas beryllium has a weaker pull, so they are more likely to leave.
The magnitude of Zeff relates to how "hard" the nucleus is pulling on those electrons. The harder the pull, the more likely it is for those electrons to stay put.
Based on our previous examples, we see that as you go across the Periodic Table, Zeff is larger. This is because these elements have the same number of core electrons (i.e same shielding effect), but, Zeff, is getting larger. As you go across the Periodic Table, only valence electrons are added, which are not very effective at shielding, since they are on the same energy level.
The shielding effect plays an important role in determining atomic radius. The tighter the "grip" the nucleus has on its electrons, the smaller the atomic radius is. As you move across the table, the radius is getting smaller. As we saw with beryllium and fluorine, Zeff is increasing, therefore the "grip" is increasing. Since the nucleus's pulling power is stronger, the electrons are being held closer together, meaning the atomic radius is getting smaller.
When we move down (from top to bottom) the periodic table, the atomic radius increases. As more energy levels are added, the distance between the outermost electrons and nucleus gets wider and wider. The shielding effect is increasing due to the extra electrons.
Now, the equation we have been using for Zeff is useful for showing the differences between elements in the same period, but it doesn't really tell the whole story. The actual Zeff also depends on electron penetration.
Electron penetration describes how close electrons in an orbital are to the nucleus. As you get closer, the electrons can "block out" the charge from electrons farther away.
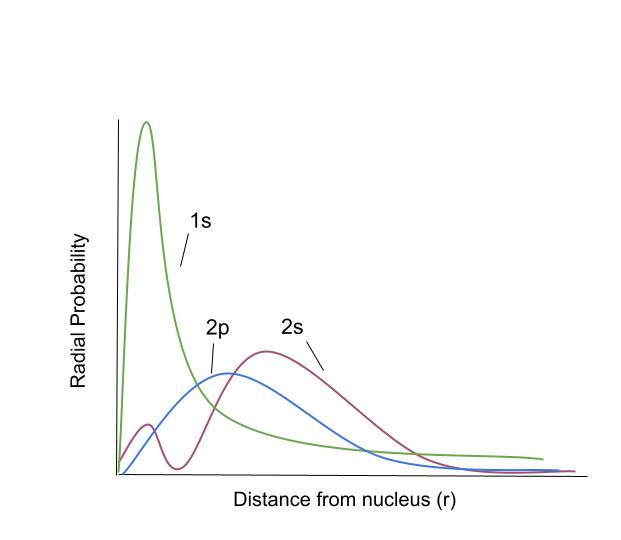
Depending on which orbital an electron is in, the probability that the electron will be a certain distance from the nucleus is based on the curves above (data is for hydrogen). StudySmarter Original.
"Radial probability" is just a fancy word for "how likely it is for an electron to be here". So for example, if an electron is in the 1s orbital, it's very likely that it's going to be close to the nucleus. Since a 2s electron is likely to be farther away, it will be shielded by the 1s electrons. For electrons in the same energy level, the penetrating power goes like this: \(s\gt p\gt d\approx f\)
For different energy levels and orbital type, it follows this pattern:
$$ 1s\gt 2s\gt 2p\gt 3s\gt 3p\gt 4s\gt 3d\gt 4p \gt 5s\gt 4d\gt 5p\gt 6s\gt 4f .... $$
Now let's compare the actual Zeff for fluorine to the one we calculated earlier. For 1s electrons, Zeff = 8.65, for 2s Zeff = 5.13, and for 2p Zeff = 5.10. So, that's pretty different from the Zeff we calculated before, which was 7 for fluorine. Our previous calculations treated all electrons as "equal", which isn't really the case. We calculate these other Zeff based on Slater's Rules.
Slater's rules are used to calculate Zeff by considering electron penetration. These rules are as follows: For s- and p- orbital electrons:
electrons within the same group shield 0.35 (except 1s, which is 0.30)
electrons within the n-1 group shield 0.85
electrons within the n-2 group or lower shield 1.00
For d- and f- orbital electrons:
These rules are used to calculate the proper shielding constant (S), and then we will plug it into our equation from before
.
Before we work on a practice problem, here's a quick refresher on Electron Configuration.
Depending on where an element is on the periodic table, its electrons will fill up the orbitals labeled moving left to right. StudySmarter Original.
You fill your orbitals starting from right to left until you reach the element you are looking at. The energy level is equivalent to the period for s- and p-orbitals. For d-orbitals it is n-1, and for f-orbitals it is n-2. Each suborbital can hold 2 electrons, s-orbitals have 1 suborbital, p-orbitals have 3, d-orbitals have 5, and f-orbitals have 7. So, for example, F has an Electron Configuration of 1s22s22p5.
Calculate the shielding constant, S, and Zeff for a 3p electron in chlorine.
Chlorine has an electron configuration of 1s22s22p63s23p5. Using Slater's rules, we can calculate S
$$0.35(7)+0.85(8)+1.00(2)=11.25$$
Now for Zeff. Chlorine's atomic number is 17, so it has 17 protons.
$$Z_{eff}=Z-S$$
$$Z_{eff}=17-11.25$$$$Z_{eff}=5.75$$
For comparison, if we treated every core electron with the same "weight", Zeff would be 7. So, the shielding effect is actually stronger when we take these rules into account.
The shielding effect describes how electrons closer to the nucleus "shield" the electrons farther away from the positive charge of the nucleus.
In fluorine there are 9 total electrons: 7 are valence electrons and 2 are core electrons. Those 2 core electrons block some positive charge of the nucleus to those 7 valence electrons.
The more core electrons, the stronger the shielding effect.
The shielding effect is only noticeably exhibited by electrons between the valence electrons and the nucleus. Other valence electrons are very weak at shielding since they are in the same energy level/orbital as the other valence electrons.
The shielding effect stays the same as you move across the periodic table since the number of core electrons stays the same. As you move down the table, it gets stronger since more core electrons have been added.
YOUR SCORE
Your score:
Already have an account? Log in
SIGNUP SIGNUPFlashcards in Shielding Effect28
Start learningWhat is the shielding effect?
The shielding effect describes how electrons closer to the nucleus "shield" the electrons farther away from the positive charge of the nucleus.
What is the Zeff for Aluminum? (Ignoring Slater's rules)
3
What is the formula for Zeff?
Zeff=Z-S
Z: atomic number/# of protons
S: number of core electrons
What does the magnitude of Zeff mean?
How strongly the nucleus is pulling on the electron. It is also called the "effective nuclear charge" that the electron is feeling.
Using Slater's rules, what is the S value for a 4s electron in Calcium (Ca)?
S=17.15
True or False: Electrons in the 2s orbital will experience the shielding effect from the 3s orbital.
False
Already have an account? Log in
How would you like to learn this content?
How would you like to learn this content?
Free chemistry cheat sheet!
Everything you need to know on . A perfect summary so you can easily remember everything.
The first learning app that truly has everything you need to ace your exams in one place
Sign up to highlight and take notes. It’s 100% free.
Save explanations to your personalised space and access them anytime, anywhere!
Sign up with Email Sign up with AppleBy signing up, you agree to the Terms and Conditions and the Privacy Policy of StudySmarter.
Already have an account? Log in
Explanations 
Exams 
Magazine 
