Has this ever happened to you? You decide to have a nice bottle of soda, but once you take the cap off, the soda erupts like a volcano, leaving your hands sticky from the frothy explosion. This happens because of the vapor pressure of carbon dioxide (CO2) that was dissolved in the soda. Shaking the soda increases the pressure, and since that pressure has no way of being released, it builds up until the bottle is opened, spilling all over you.
In this article, we will be learning all about vapor pressure: what it is, what factors influence it, and how to calculate it.
- This article is about vapor pressure.
- First, we will define vapor pressure and learn how it occurs.
- Next, we will learn about the factors that influence it.
- Then, we will discuss the vapor pressure of water and how it affects relative humidity.
- Lastly, we will learn how to calculate vapor pressure in different situations.
Vapor Pressure Definition
Let's start by looking at the definition of vapor pressure.
When a liquid and its gas form are in a closed container, the pressure exerted by the gas is called vapor pressure.
When a liquid and its gas are in a closed container, they exist in equilibrium. No matter the temperature, some liquid particles will have enough energy to enter the gas phase.
Causes of Vapor Pressure
Now, let's explore the causes of vapor pressure. Vapor pressure is caused by gas particles colliding with the walls of the container. Here is a diagram to illustrate:
Gas particles collide with the container to create vapor pressure. StudySmarter Original.
Since this is at equilibrium, liquid is evaporating into gas, and gas is condensing into liquid.
When the vapor pressure is equal to the atmospheric pressure, boiling occurs. Since the liquid isn't being "held down" by the atmospheric pressure, the liquid can escape and spread out as a gas.
Factors that Affect Vapor Pressure
Two main factors that affect vapor pressure. These are:1. Temperature2. Type of molecule
Increasing the temperature will increase the vapor pressure. This is because more molecules have the energy to escape from the liquid phase into the gas phase.
The type of molecule will also affect vapor pressure. More specifically, the forces between the molecules affect vapor pressure. When molecules have strong forces between them, the vapor pressure is low, since these forces make it harder for molecules to become gaseous. For a liquid to become a gas, the forces between molecules are severed, so the stronger the forces, the harder it is to become a gas.
Vapor Pressure of Water
When we talk about vapor pressure, we are often referring to water. The vapor pressure is often utilized in one of two ways:1. Determining boiling point2. Relative humidityWhen we refer to the boiling point of water, we are typically talking about the boiling point at 1 atm (atmospheric pressure at sea level). However, this boiling point changes depending on what the atmospheric pressure is, since boiling occurs when vapor pressure = atmospheric pressure. For example, at 10,000 feet (ca. 3 km) above sea level, the atmospheric pressure is only about 0.69 atmospheres. Since there is less "push" from the atmosphere, the boiling point is lowered.
Relative humidity is also related to vapor pressure.
Relative humidity is the ratio of the partial pressure (how much pressure a species contributes) of water to the equilibrium vapor pressure. The formula is: $$\text{Relative humidity}=\frac{\text{partial pressure}}{\text{vapor pressure}} * 100\%$$
The relative humidity tells us how much water vapor is in the air versus how much the air can "hold" at that temperature. If you have ever seen humidity listed as a percent before, this is what that means. Let's work on an example.
At 25°C, the vapor pressure of water is 0.0313 atm. If the partial pressure of the water vapor in the air is 0.0211 atm, what is the relative humidity?
To calculate the relative humidity, we just divide the vapor pressure by the partial pressure of the water vapor.
$$\text{Relative humidity}=\frac{\text{partial pressure}}{\text{vapor pressure}} * 100\%$$
$$\text{Relative humidity}=\frac{0.0211\,atm}{0.0313\,atm}*100\%=67.4\%$$
Vapor Pressure Formulas
There are three main formulas associated with vapor pressure:1. Clausius-Clapeyron2. Raoult's Law3. Henry's Law
Let's start with the Clausius-Clapeyron formula.
The Clausius-Clapeyron formula shows the relationship between vapor pressure and temperature. The formula is: $$ln\frac{P_2}{P_1}=\frac{\Delta H_{vap}}{R}(\frac{1}{T_1}-\frac{1}{T_2})$$Where: P1 is the partial pressure at T1, P2 is the partial pressure at T2, ΔHvap is the enthalpy of vaporization (net energy it takes to go from a liquid to a gas), and R is the ideal gas constant
We commonly use this formula to calculate the change in vapor pressure due to a temperature change. Here's a graph for water:
The vapor pressure of water increases with temperature. StudySmarter
The increase in vapor pressure is exponential, so the greater the temperature, the larger the change in vapor pressure. Clausius-Clapeyron can exclusively be used for pure substances.
If we want to look at vapor pressure for a mixture, that's where Raoult's law comes in.
Raoult's law is used to calculate the total vapor pressure of a solution composed of two or more liquids with different vapor pressures. The formula is:
$$P_{total}=\sum_{i} P_i \chi_i $$
Where Pi is the vapor pressure of a given substance and χi is the mole fraction of that substance
The mole fraction is the ratio of one substance to the whole solution. The formula is:$$\chi=\frac{n_i}{n_{tot}}$$
Where ni is the number of moles of one substance and ntot is the total amount of moles in the solution.
Here's a graph showing how Raoult's law works.
Vapor pressure changes based on mole fraction. StudySmarter Original.
A lot is going on in the diagram, so let's break it down.
The pink line represents the partial pressure of species A. On the left, the mole fraction of A is one, so the whole solution is just A. This means that the total pressure is equal to the pure vapor pressure of A (PA°). As the mole fraction of A decreases, the partial pressure also decreases until it is 0.
The green line is the partial pressure of species B. On the right, the mole fraction of B is one, so the whole solution is B. This also means that Ptotal=PB°. The partial pressure decreases as you move to the left, since the mole fraction is also decreasing.
Lastly, the black line is the total pressure. As mentioned previously, if only one species is present, the total pressure is equal to the vapor pressure of that pure substance.
Our last formula is Henry's law.
Henry's law is used when a liquid contains a solute (dissolved species). This law can be used for both non-volatile (will not evaporate) and volatile (will evaporate) solutes. The formula is:
$$C=(K_H)P_{gas}$$
Where KH is Henry's constant, C is either the solubility, concentration, or mole fraction of the gas, and P is the pressure of the gas.
The units/value of Henry's constant depends on what C represents.
While C can represent a few different things, the relationship between C and P stays the same. Solubility, mole fraction, and concentration all tell us the same thing: how much of the solute is in the liquid. The relationship between C and P is dependent on whether the solute is volatile or not.Here is a diagram showing these relationships:
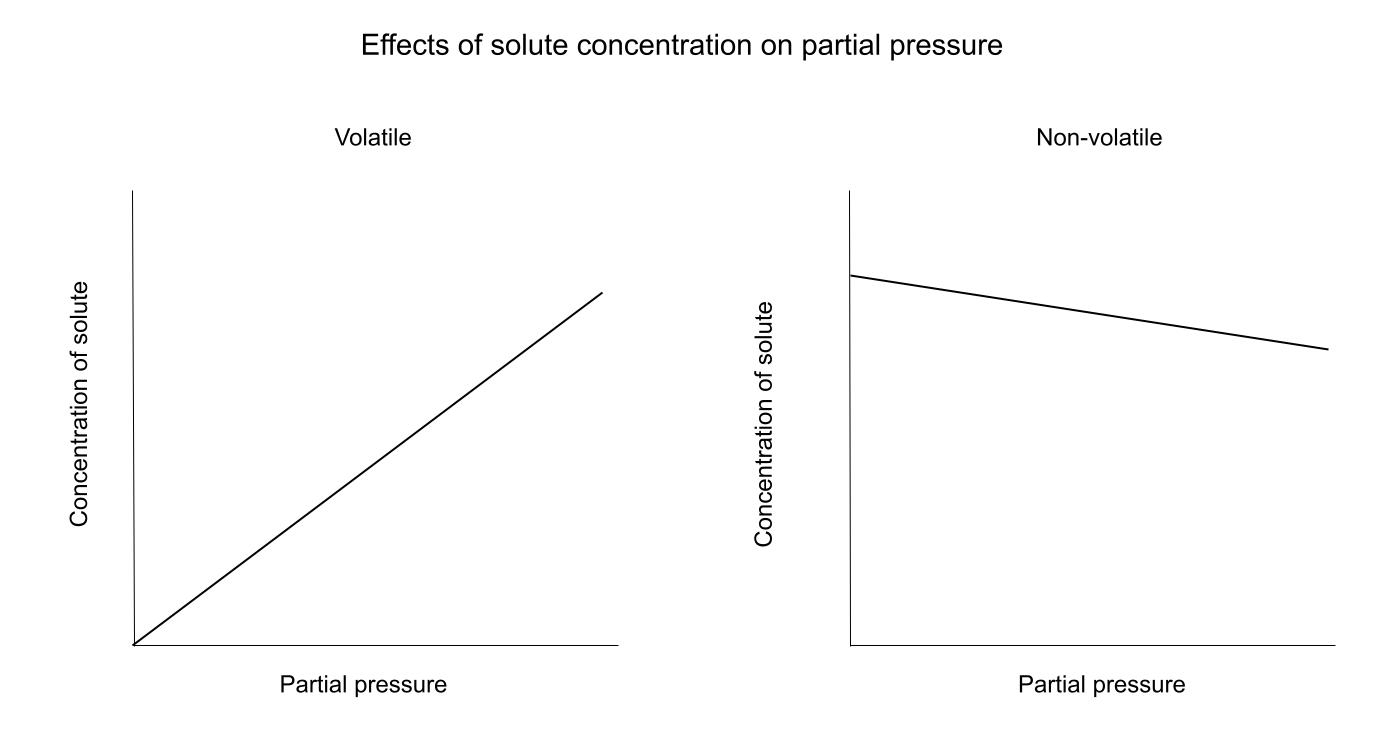
For a volatile solute, an increase in C (all types) leads to an increase in pressure. This is because the more volatile particles in solution, the more particles that can evaporate and become gaseous.For a non-volatile solute, the relationship is the opposite. The solute particles are "in the way" of the solvent particle's path to the surface to become a gas. Think of it like walking through a crowd, the more people there are, the harder it is to find an easy pathway to your destination.
Henry's law can explain a disease called "the bends" (decompression sickness). When a scuba diver goes deep into the ocean, the pressure increases. This increase in pressure leads to gases like nitrogen being more soluble in the blood. If a diver rises too quickly, the rapid change in pressure causes these gases to rapidly condense and form bubbles.
These bubbles can cause the blood vessels to pop, which leads to "the bends" and a lot of pain and medical issues for the diver. To avoid this, divers rise slowly so the gas in the blood can equilibrate with the external pressure, preventing these bubbles.
Vapor Pressure Examples
Now that we've covered the different equations, let's work on some examples.
The vapor pressure of water at 303 K is 0.0418 atm. What is the vapor pressure of water at 363 K? The enthalpy of vaporization (ΔHvap) for water is 44,000 J/mol and the gas constant is 8.315 J/molK.Since we are looking at the change in pressure with temperature, we will use the Clausius-Clapeyron formula. All we need to do is plug in our values and solve for P2.
$$ln\frac{P_2}{P_1}=\frac{\Delta H_{vap}}{R}(\frac{1}{T_1}-\frac{1}{T_2})$$$$ln\frac{P_2}{0.0418\,atm}=\frac{44,000\frac{J}{mol}}{8.315\frac{J}{molK}}(\frac{1}{303\,K}-\frac{1}{363\,K})$$$$ln\frac{P_2}{0.0418\,atm}=(5,291\,K)(0.000546\,K^{-1})$$$$ln\frac{x}{y}=ln(x)-ln(y)\,\,\text{(rule we use to simplify equation)}$$$$ln(P_2)-ln(0.0418\,atm)=2.89$$$$ln(P_2)=2.89+(-3.17)$$$$e^{ln(P_2)}=e^{-0.28}$$$$P_2=0.756\,atm$$
A solution consists of 0.35 mol water, 0.62 mol ethanol, and 0.15 mol butanol. The partial pressures at 298 K are (in order): 0.0313 atm, 0.0579 atm, and 0.0893 atm. What is the total vapor pressure of the solution?
Since we are looking at a solution of three liquids, we will use Raoult's law. Our first step is to calculate the mole fraction of each species.|
$$\chi_i=\frac{n_i}{n_{tot}}$$$$n_{tot}=0.35\,mol+0.62\,mol+0.15\,mol=1.12\,mol$$$$\chi_{water}=\frac{0.35\,mol}{1.12\,mol}=0.313$$$$\chi_{ethanol}=\frac{0.62\,mol}{1.12\,mol}=0.554$$$$\chi_{butanol}=\frac{0.15\,mol}{1.12\,mol}=0.133$$Next, we multiply each species' partial pressure by their mole fraction, and add these values together to get the total vapor pressure.$$P_{total}=\sum_{i} P_i \chi_i $$$$P_{total}=(P_{water}* \chi_{water})+(P_{ethanol}* \chi_{ethanol}+(P_{butanol}* \chi_{ethanol})$$$$P_{total}=(0.0313\,atm*0.313)+(0.0579\,atm*0.554)+(0.0893\,atm*0.133)$$$$P_{total}=0.0538\,atm$$
In a 2 L bottle of soda, the concentration of dissolved CO2 is 0.0875 M. If the Henry's law constant for CO2 at 25 °C is 3.1x10-2 M/atm, what is the partial pressure of the CO2?
Since we are talking about a solute (CO2), we will be using Henry's law. All we need to do is plug in our variables and solve for pressure.
$$C=(K_H)P_{gas}$$
$$P_{gas}=\frac{C}{K_H}$$$$P_{gas}=\frac{0.0875\,M}{3.1x10^{-2}\frac{M}{atm}}$$
$$P_{gas}=2.82\,atm$$
Vapor Pressure - Key takeaways
- When a liquid and its gaseous state are in a closed container, the pressure exerted by the gas is called vapor pressure.
- Vapor pressure is caused by gas particles colliding with the walls of the container.
- Two main factors that affect vapor pressure:1. Temperature (Increase in temperature = increase in pressure)2. Type of molecule (the stronger the forces between molecules, the weaker the vapor pressure)
- Relative humidity is the ratio of the partial pressure (how much pressure a species contributes) of water to the equilibrium vapor pressure. The formula is: $$\text{Relative humidity}=\frac{\text{partial pressure}}{\text{vapor pressure}} * 100\%$$
- The Clausius-Clapeyron formula shows the relationship between vapor pressure and temperature. The formula is:$$ln\frac{P_2}{P_1}=\frac{\Delta H_{vap}}{R}(\frac{1}{T_1}-\frac{1}{T_2})$$
- Raoult's law is used to calculate the total vapor pressure of a solution composed of two or more liquids with different vapor pressures. The formula is:
$$P_{total}=\sum_{i} P_i \chi_i $$
Henry's law is used when a liquid contains a solute (dissolved species). This law can be used for both non-volatile (will not evaporate) and volatile (will evaporate) solutes. The formula is:
$$C=(K_H)P_{gas}$$
Explanations 
Exams 
Magazine 
