A projectile motion takes place when an object moves in the air and is under the influence of gravity.
This motion is always curved – it follows a parabolic trajectory. In addition, objects carrying out a projectile motion are pulled by gravitational force and therefore must hit the ground.
Examples of projectiles
Real-life examples of projectile motions are:
The movement of a bullet shot from a gun.
The movement of cannonballs.
Throwing a javelin.
Casting a stone.
Jumping into a swimming pool.
Types of projectile motion
There are two types of projectile motion – horizontally shot projectiles, and non-horizontally shot projectiles.
Horizontally shot projectiles
This takes place when an object is launched in a horizontal direction from a height above the ground. From this elevation, the object follows a curved path before hitting the ground. An example of a horizontally shot projectile is a bullet shot from a gun in the horizontal direction.
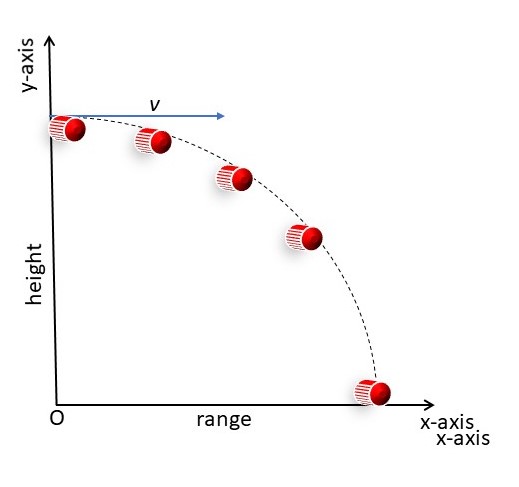
A horizontally shot projectile. Image: Njoku, StudySmarter Originals
Non-horizontally shot projectiles
This occurs when an object is launched from the ground or from a height above the ground upwards, giving rise to a complete parabolic motion. An example of a non-horizontally shot projectile is a rocket projected vertically from the ground.
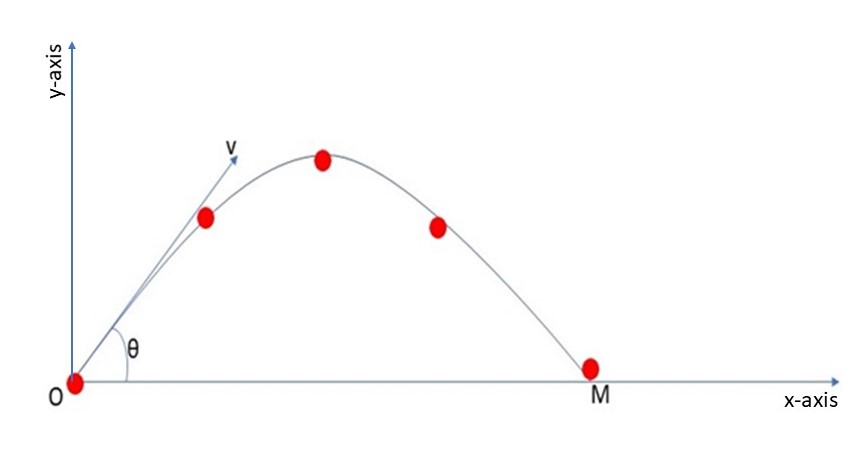
A non-horizontally shot projectile. Image: Njoku - StudySmarter Originals
Components of a projectile
Projectile motion is best understood when split into two components: horizontal and vertical.
If a ball B is launched from the ground at a point G, the position of the ball along the curved path before it hits the ground can be given as the coordinates (x, y).

The pathway and components of a projectile. Image: Njoku - StudySmarter Originals
Remember that the ball moves at velocity v, and at an angle θ to the horizontal. To find the horizontal component of the velocity x and vertical component y, we apply Pythagoras' theorem. Then:
\[v_x = v \cdot \cos \theta\]
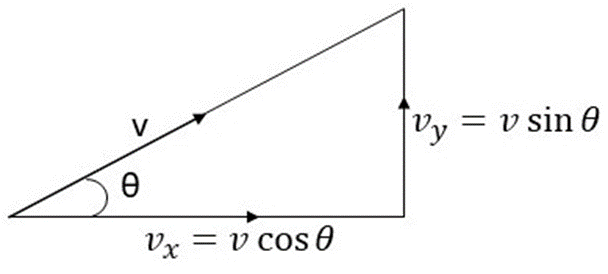
The resolution of velocity into the vertical and horizontal components, Njoku - Study Smarter Originals The equation \(v_x = v \cdot \cos \theta\) is regarded as the horizontal component of the velocity in the projectile motion while the equation \(v_y = v \cdot \sin \theta\) is the vertical component of the velocity.
To further determine the horizontal component of the motion, we apply SUVAT equations.
Remember:
\[S = ut +\frac{1}{2} at^2\]
Note that for horizontal motion there is no acceleration, thus a = 0.
So, the horizontal component of a projectile motion is:
\[x = u \cos \theta \cdot t + \frac{1}{2} \cdot 0 \cdot t^2\]
Remember that the velocity u is replaced with the horizontal component of the velocity of the object.
Thus: \(x = ut \cdot \cos \theta\) is the equation of the horizontal component of a projectile motion.
However, to determine the vertical component, you should note that the object initially moves upwards. This means that its acceleration is in the opposite direction of gravity, so:
\[a = - g = -9.8 \frac{m}{s^2}\]
Also, note that the value of u in this case is the vertical component of the velocity of the object. So, the vertical component of a projectile motion is:
\[y = u \sin \theta \cdot t + (-g) \cdot \frac{1}{2} t^2\]
Thus: \(y = ut \sin \theta -g \frac{1}{2} t^2\) is the vertical component equation of the projectile motion.
Understanding these equations along with a basic knowledge of the general equations of motion is important.
Time of flight, range, and maximum height
In projectile motion questions, you will need to calculate the range, maximum height, and time of flight. A step-by-step approach helps you understand how to solve these in this text.
What is the time of flight of a projectile?
The time of flight of a projectile is the total time taken from the point at which the object is launched to the point it hits the ground. It is denoted with the symbol T.
Recall that: \(v - u = at\) is the first equation of motion. Note that the time of flight is the time taken for the object to go up and down until it hits the floor. We have to consider the vertical component of the projectile motion.
To best understand the motion, we divide it into two levels. The first level covers when the object is launched from its starting point (the ground) to the maximum height. Then, the second level covers the motion from the maximum height to the point it drops to the launch level (the ground).
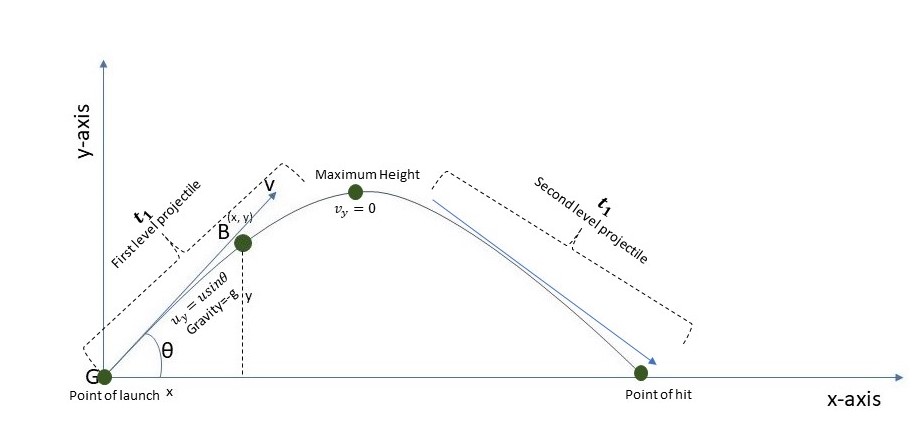
An illustration on the time of flight of a projectile, Njoku - StudySmarter Originals\(v_y - u_y = -g \cdot t_1\)
Remember that: \(v_y = 0, \space u_y = u \sin \theta\)
\(-u \sin \theta = -gt\)
\(t = \frac{u \sin \theta}{g}\)
Thus, time of flight T is:
\(T = \frac{ 2u \sin \theta}{g}\)
Peter launched a rocket at an angle of 30 degrees to the horizontal. The rocket moved at a velocity of 500 m/s. Calculate:
The time of flight.
The time it takes to get to the maximum height.
Take \(g = 9.8 \space m/s^2\)
Solution:
θ = 30 °
u = 500 m/s
g = 9.8 m/s2
Time of flight is calculated as:
\(T = \frac{2 u \sin \theta}{g} \quad T = \frac{2 \cdot 500 ms^{-1} \cdot \sin30^\circ}{9.8 ms^{-2}} \quad T = \frac{1000 ms^{-1} \cdot 0.5}{9.8 ms^{-2}}\)
\(T = 51.02 s\)
The time it takes the rocket to reach its maximum height is t.
\(T = 2t\)
\(t = \frac{T}{2}; \space t = \frac{51.02 s}{2} = 25.51 s\)
What is the range of a projectile motion?
The range of a projectile motion is known as the total horizontal distance travelled by the object from the point it is launched, to the point it hits the ground. R is used to represent the range. The range is calculated by finding the product of the velocity at the horizontal direction and the time of flight.
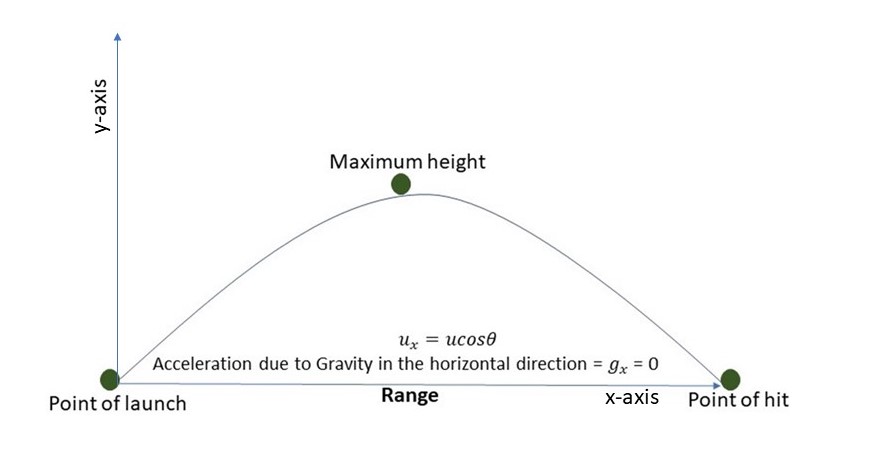
Range of a projectile, Njoku - StudySmarter Originals\(R = u_x \cdot T\)
Remember that: \(u_x = u \cos \theta\).
Do not forget the range is the horizontal distance of the projectile.
Note that:
\(T =![]() \frac{2u \sin \theta}{g}\)
\frac{2u \sin \theta}{g}\)
\(R = u \cos \theta \cdot \frac{2 u \sin \theta}{g}\)
In trigonometry: \(\sin (2\theta) = 2\sin\theta \cos\theta\)
Thus: \(R = \frac{u^2 \sin(2 \theta)}{g}\)
As the formula in calculating the range contains 2θ it means that the highest value of the range at 45°, which means \(\sin (2 \theta) = sin(90^\circ) = 1\).
In a football match, a goalkeeper kicks a stationary ball. If the ball moves at a velocity of 27 m / s and 30 ° to the ground, calculate the range. Take g = 9.8 m / s²
Solution:
u = 27 m / s
θ = 30 °
g = 9.8 m / s²
\(R = \frac{u^2 \sin 2 \theta}{g} = \frac{(27 ms^{-1})^2 \cdot \sin(2 \cdot 30^\circ)}{9.8 ms^{-2}} = \frac{(27 ms^{-1})^2 \cdot \sin 60^\circ}{9.8 ms^{-2}}\)
R = 64.42 m
What is the maximum height of a projectile?
The maximum height is the highest point the object reaches while moving upwards before it begins to drop. At the maximum height, the object suspends shortly before it starts a downward movement. At this level, the velocity is zero in the vertical direction.
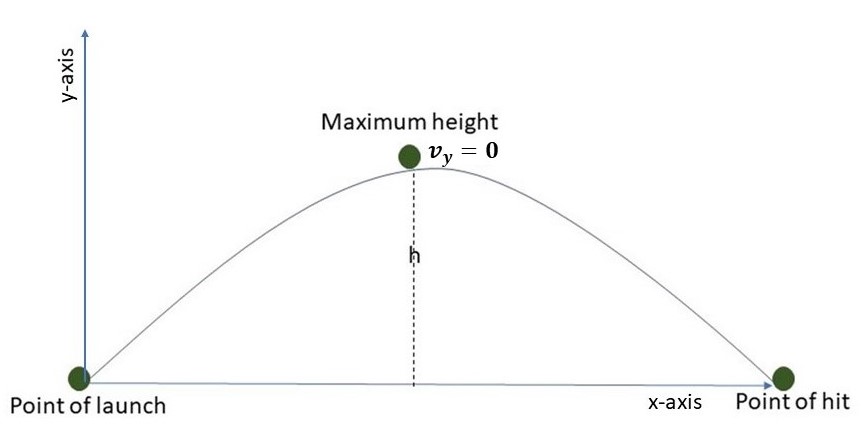
An illustration of the maximum height of a projectile motion, Njoku - StudySmarter
In order to calculate the maximum height, the velocity in the vertical direction is \(u_y = u \sin \theta\).
Remember the equation of motion: \(v^2 - u ^2 = 2a \cdot S\)
Where: v = 0, S = h, a = -g.
\(-u_y^2 = -2gh\)
So:
\(h = \frac{y_y^2}{2g}\)
\(h = \frac{(u \sin \theta)^2}{2g}\)
Thus, the maximum height of a projectile is:
\(h = \frac{u^2 \sin^2 \theta}{2g}\)
A dynamite rocket was launched with a velocity of 200 m/s at an angle of 60 degrees to the horizontal. What is the highest height attained by the dynamite? Take g = 9.8 m/s2
Solution:
u = 200 m / s
θ = 60°
g = 9.8 m / s²
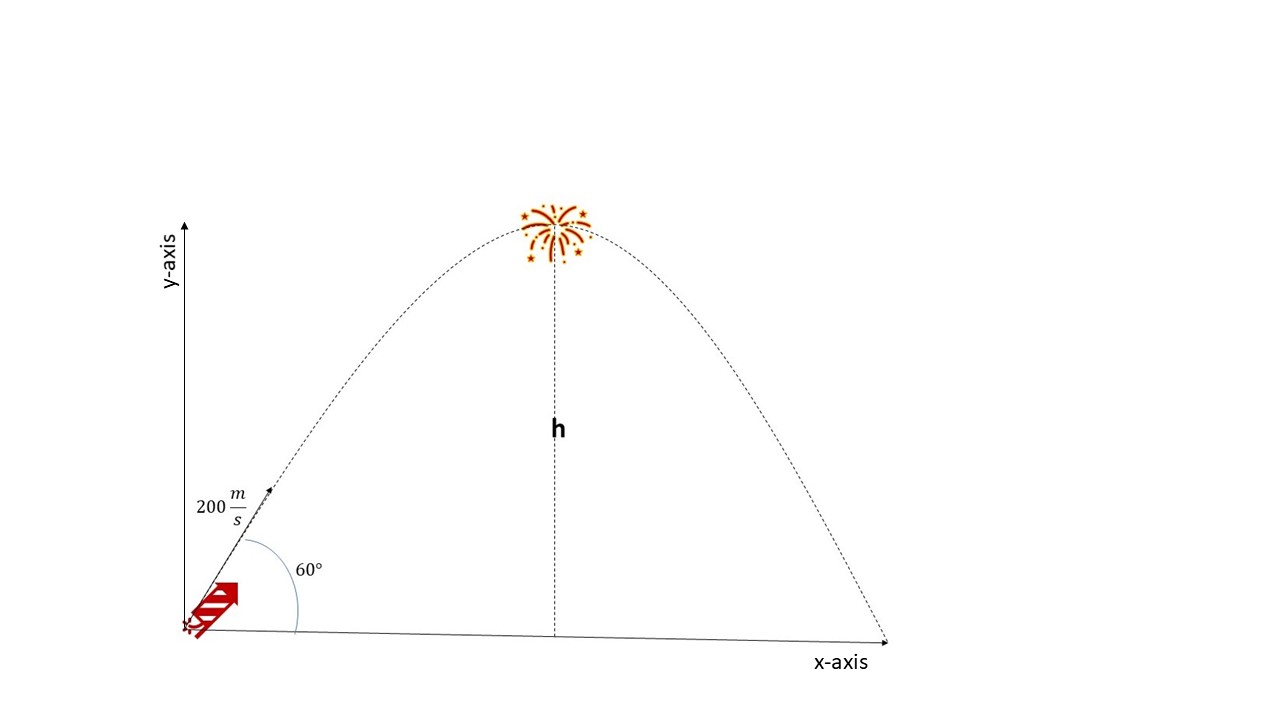
An example of dynamite in a projectile motion, Njoku - StudySmarter Originals
\(h = \frac{u^2 \sin^2 \theta}{2g} = \frac{(200 ms^{-1})^2 \sin^2 60^\circ}{2 \cdot 9.8 ms^{-2}} = \frac{40000 (ms^{-1})^2 \cdot 0.75}{19.6 ms^{-2}}\)
h = 1530.61 m
How to calculate projectiles using vectors
You solve projectile questions using vectors by understanding the quantities which are vectors. In this case, only the acceleration, velocity and displacement are vectors. For vector quantities, the horizontal component i and vertical component j are always represented.
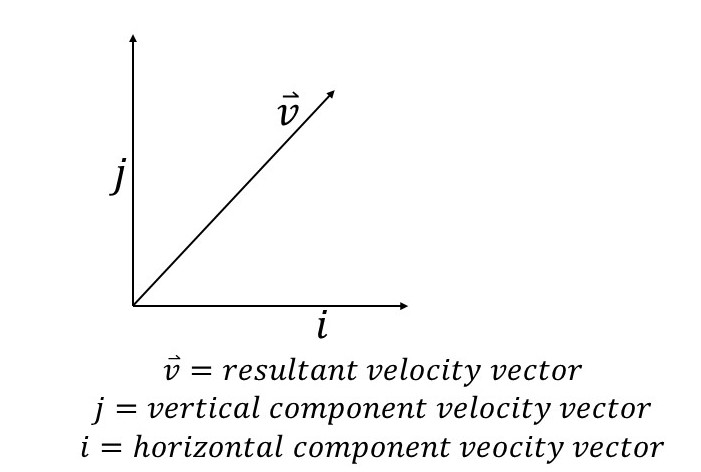
An image showing vectors and their direction, Njoku - StudySmarter OriginalsFor a vector 5i, it means that the quantity is 5 units in the positive horizontal direction (to the right on the x-axis). But for a vector -3j, it means that the quantity is 3 units in the negative vertical direction (in a downwards direction on the y-axis).
The vector direction is given in place of an angular direction in degrees. You will be relying on the displacement and velocity equations:
\(S = S_0 + ut + \frac{1}{2} at^2\)
\(v = u + at\)
Where S = displacement,
S0 = initial displacement
a = acceleration
t = time,
v = final velocity and
u = initial velocity.
A tennis ball is struck by a paddle from a point K, 10m above the point O on the ground. At that instant, it moves with a velocity (4i + 7j) m/s. Eventually, it hits point M on the ground after moving freely under gravity. Take g = 9.8 m/s².
Determine the speed of the ball 1.8 seconds after being struck.
Derive a vector expression for a point S of the tennis ball which is relative to O at time t seconds.
Find the distance OM.
Solution:
Make a diagram of the information from the question.
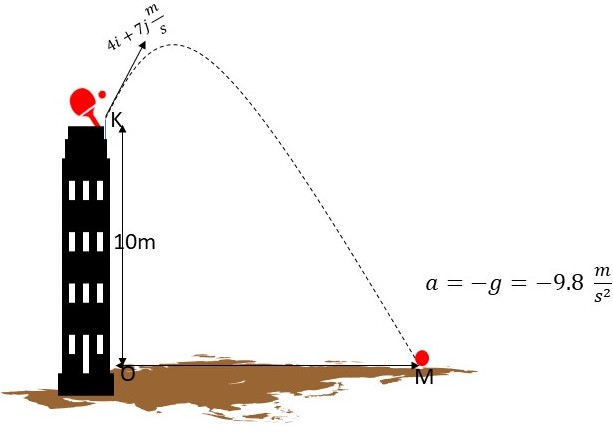
An image of a tennis ball hit from the top of a building, Njoku - StudySmarter Originals1. Refer to the equation: v = u + at
v =?
u = 4i + 7j in m/s
a = -9.8j in m/s²
because the tennis ball accelerates vertically in the opposite direction of gravity, t = 1.8 in seconds
Substitute your values into the equation:
v = 4i + 7j + (-9.8j) × 1.8
v = 4i + 7j - 17.64j
v = 4i - 10.64j
To calculate v, you need to find the resultant of the vector 4i - 10.64j. This is calculated by finding the square root of the sum of the squares of both the horizontal component 4i and vertical component 10.64j.
\(v = \sqrt{4^2 + 10.64^2} m/s = 11.37 m/s\)
2. To derive a vector expression for a point S of the tennis ball which is relative to O at time t seconds, the following equation is used:
\(S = S_0 + ut + \frac{1}{2} at^2\)
Here,
S =?
S0 = 10j metres because the initial vertical displacement of the tennis ball is 10 m above the ground,
u = 4i + 7y in m/s,
t = t in seconds,
a = -9.8j in m/s²
Thus:
\(S = 10 j + (4i + 7j)t + \frac{1}{2} (-9.8j)t^2 \quad S = 10 j + 4 ti + 7tj -4.9t^2 j\)
Bring similar vector components together to factorise: \(S = 4ti + 10j+7tj-4.9t^2j \quad S = 4ti + (10 + 7t - 4.9t^2)j\)
So, the equation to determine a distance S from the point O where the tennis ball was struck is: \(S = 4ti + (10 + 7t - 4.9 t^2)j\)
3. To find the displacement OM, the point M has no vertical distance since the egg hits the ground at M. So, the vertical component of the vector representation is + 0j.
Refer back to the equation derived in B – remember that it tells us how to find the displacement of any point from the origin O.
\(S = 4ti + (10 + 7t - 4.9t^2)\)
Since point M has no vertical component, \((10 + 7t - 4.9 t^2)j = 0 \space 10 + 7t - 4.9t^2 = 0\)
Using the general quadratic equation \(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\) we can calculate the time t at which the tennis ball hits the ground M.
From the equation \(10 + 7t - 4.9 t^2 = 0\)
a = -4.9,
b = 7
c = 10
If you substitute your values into that formula you would have values:
t = 2.31s or -0.88s.
Note that only the positive value of t is taken because a negative value would mean that the tennis ball travelled back in time.
So, t = 2.31s.
This means that the tennis ball hits the point M after 2.31 seconds. To determine the horizontal displacement OM, we would substitute the value of t in: \(S = 4ti + (10 + 7t - 4.9t^2)j\)
Do not forget that the vertical component is zero, therefore:
S = 4ti
Where t = 2.31s
S = 4 × 2.31i
S = 9.24i
Thus, the distance OM is 9.24m.
Projectiles - key takeaways
- A projectile motion occurs when a body moves freely in air under the influence of gravity.
It is assumed no other force acts on the object except gravity.
Projectiles can be horizontally shot or non-horizontally shot.
The velocity in the y-direction is given as \(v_y = v \sin \theta\) while that of the x-direction is \(v_x = v \cos \theta\).
The time of flight is the total time taken for an object to complete a projectile motion. It is given as: \(T = \frac{2u \sin \theta}{g}\)
The range is the horizontal distance from the point of launch to the point the projectile strikes the ground. It is given as: \(R = \frac{u^2 \sin 2 \theta}{g}\)
The maximum height is the vertical distance between the peak height reached by the projectile and the ground. At the maximum height, the final velocity is zero and it is given as: \(h = \frac{u^2 \sin^2 \theta}{2g}\)
To calculate projectiles using vectors, the horizontal and vertical components of all vector quantities must be involved. The following displacement and velocity equations are used: \(S = S_0 + ut + \frac{1}{2} at^2\) and \(v = u + at\)
Related topics to Mechanics Maths
How we ensure our content is accurate and trustworthy?
At StudySmarter, we have created a learning platform that serves millions of students. Meet
the people who work hard to deliver fact based content as well as making sure it is verified.
Content Creation Process:
Lily Hulatt is a Digital Content Specialist with over three years of experience in content strategy and curriculum design. She gained her PhD in English Literature from Durham University in 2022, taught in Durham University’s English Studies Department, and has contributed to a number of publications. Lily specialises in English Literature, English Language, History, and Philosophy.
Get to know Lily
Content Quality Monitored by:
Gabriel Freitas is an AI Engineer with a solid experience in software development, machine learning algorithms, and generative AI, including large language models’ (LLMs) applications. Graduated in Electrical Engineering at the University of São Paulo, he is currently pursuing an MSc in Computer Engineering at the University of Campinas, specializing in machine learning topics. Gabriel has a strong background in software engineering and has worked on projects involving computer vision, embedded AI, and LLM applications.
Get to know Gabriel

















