Any real-life scenario containing unknown quantities can be modelled into mathematical statements. For instance, say you wanted to model the population of eagles and frogs in a particular habitat. Each year, the population of frogs double while the population of eagles halves. By creating a suitable expression that describes the decrease of eagles and the increase of frogs in this ecosystem, we can make predictions and identify trends in their population.
In this article, we will discuss expressions, what they look like, and how to factorise and simplify them.
Defining an Expression
An expression can be used to describe a scenario when an unknown Number is present or when a variable value exists. It helps solve real-world problems in a more simplified and explicit manner.
A variable value is a value that changes over time.
To construct an expression of this kind, you would need to determine which quantity is unknown in the circumstance, and then define a variable to represent it. Before we dive into this topic further, let us first define expressions.
Expressions are mathematical statements that have two terms at least that contain variables, numbers, or both. Expressions are such that they contain also at least, one mathematical operation; addition, subtraction, multiplication, and division.
Let's see an example of an expression.
The following is a mathematical expression,
\[2x+1\]
because it contains one variable, \(x\), two numbers, \(2\) and \(1\), and one mathematical operation, \(+\).
Expressions are very organised, in a way that a statement that has an operator come right after another one is not a valid expression. For example,
\[2x+\times 1.\]
They are also organised in the sense that when a parenthesis opens, there needs to be a close. For example,
\[3(4x+2)-6\]
is a valid expression. However,
\[6-4(18x\]
is not a valid expression.
Components of an Expression
Expressions in Algebra contain at least a variable, numbers, and an arithmetic operation. However, there are quite a Number of terms related to the parts of an expression. These elements are described below.
Variables: Variables are the letters that represent an unknown value in a mathematical statement.
Terms: Terms are either numbers or variables (or numbers and variables) multiplying and dividing each other and are separated by either the addition (+) or subtraction sign (-).
Coefficient: Coefficients are the numbers that multiply variables.
Constant: Constants are the numbers in expressions that do not change.
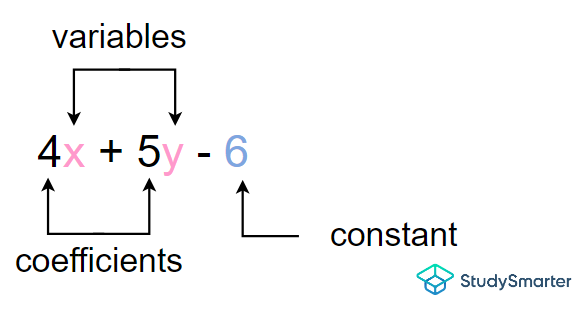
Components of an expression
Examples of Expressions
Here are some examples of mathematical expressions.
1) \((x+1)(x+3)\)
2) \(6a+3\)
3) \(6x-15y+12\)
4) \(y^2+4xy\)
5) \(\frac{x}{4}+\frac{x}{5}\)
Notice that all of them contain the necessary components to be considered expressions. They all have variables, numbers, and at least one mathematical operation composing them.
In particular, in the first example, you will find a multiplication implicit in the parenthesis that connects the two terms \(x+1\) and \(x+3\); so it is a valid expression. In the fourth example, in the second term, variables \(x\) and \(y\) are multiplying and it's written as \(xy\). So, that one is also a valid expression.
Writing Expressions
In this segment of our discussion, we will be introduced to writing expressions, particularly translating word problems into mathematical ones. Such skill is important when solving a given question. By doing so, we can visualise anything in terms of numbers and arithmetic operations!
Translating Word Problems into Expressions
Given a sentence that illustrates a mathematical statement, we can translate them into expressions that involve the appropriate components of expressions we had mentioned before and mathematical symbols. The table below demonstrates several examples of word problems that have been translated into expressions.
Phrase | Expression |
Five more than a number | \[x+5\] |
Three-fourths of a number | \[\frac{3y}{4}\] |
Eight larger than a number | \[a+8\] |
The product of a number with twelve | \[12z\] |
The quotient of a number and nine | \[\frac{x}{9}\] |
Types of Maths Expressions
Numerical Expressions
In comparison to what expressions are, there are expressions that do not contain variables. These are called numerical expressions.
Numerical expressions are a combination of numbers with mathematical operators separating them.
They could be as long as possible, containing as many mathematical operators as possible also.
Here are a few examples of numerical expressions.
1) \(13-3\)
2) \(3-7+14-9\)
3) \(12+\frac{4}{17}-2\times 11+1\)
4) \(4-2-1\)
Algebraic Expressions
Algebraic expressions are expressions that contain unknowns. Unknowns are variables that are often represented by letters. In most cases throughout our syllabus, these letters are \(x\), \(y\) and \(z\).
However, we may sometimes get expressions that comprise Greek letters as well. For instance, \(\alpha\), \(\beta\) and \(\gamma\). Below are several examples of algebraic expressions.
1) \(\frac{2x}{7}+3y^2\)
2) \(4\alpha-3\beta + 15\)
3) \(x^2+3y-4z\)
Evaluating Maths Expressions
In this section, we will be introduced to evaluating math expression. Here, we would essentially solve a given expression based on the arithmetic operations between the numbers or variables. These basic arithmetic operations (or mathematical symbols) include Addition, Subtraction, Multiplication and Division. We will also see how these operations can help us factorise and simplify such expressions.
Addition and Subtraction of Expressions
Addition and subtraction are the primary actions done when adding and subtracting Fractions. These are performed on like terms. There are two steps to consider here, namely
Below is a worked example.
Add the expressions \(5a-7b+3c\) and \(-4a-2b+3c\).
Solution
Step 1: We will first put the two expressions together so we can rearrange them.
\[5a-7b+3c+(-4a-2b+3c)\]
Then,
\[5a-7b+3c-4a-2b+3c\]
Next,
\[5a-4a-7b-2b+3c+3c\]
Step 2: We can now successfully add all the like terms.
\[a-9b+6c\]
Here is another worked example for you.
Add the expressions
\(7x^2+8y-9y\), \(3y+2-3x^2\) and \(3-y+3x^2\).
Solution
Step 1: We will note them down so that they can be rearranged
\[7x^2+8y-9+3y+2-3x^2+3-y+3x^2\]
Then,
\[7x^2+3x^2-3x^2+8y-y+3y-9+2+3\]
Step 2: Add the like terms
\[7x^2+10y-4\]
Factorising Expressions
This is an important element when it comes to dealing with expressions. It helps us group like terms in order for us to perform arithmetic operations more structured manner.
Factorising is the process of reversing the expansion of brackets.
The factorised form of expressions is always in brackets. The process involves taking out the highest Common Factors (HCF) from all the terms such that when the Factors are taken out and multiplied by the values in the brackets, we will arrive at the same expression we had in the first place.
For example, say you had the expression below.
\[4x^2+6x\]
Notice here that the coefficients of \(x^2\) and \(x\) both have a factor of 2 since 4 and 6 are divisible by 2. Furthermore, \(x^2\) and \(x\) have a common factor of \(x\). Thus, you can take these two Factors out of this expression, making the factories form equivalent to
\[2x(2x+3)\]
Let's explain this again with another example.
Factorise the expression
\[6x+9\]
Solution
To factorise this we need to find the HCF of \(6x\) and 9. That value happens to be 3. Therefore, we will note down the value and account for the bracket.
\[3(?+?)\]
The sign in the bracket above is gotten from the sign in the initial expression. To find out what values must be in the brackets, we will divide the terms in the expressions that we factorised the 3 from by the 3.
\[\frac{6x}{3}=2x\]
and
\[\frac{9}{3}=3\]
Then, we will arrive at
\[3(2x+3)\]
We can evaluate to see if the answer we have is right by expanding the brackets.
\[(3\times 2x)+(3\times 3)=6x+9\]
as we had before!
Let's go through one more example.
Simplify the expression
\[3y^2+12y\]
Solution
We will need to find the HCF. Usually, these can be broken down just if they are a bit too complex at first. Looking at the coefficients, we realise that 3 is the HCF. That will be taken outside the bracket.
\[3(?+?)\]
We can now divide the expression from which the 3 was factored by the 3.
\[\frac{3y^2}{3}=y^2\]
and
\[\frac{12y}{3}=4y\]
This leaves us with the expression;
\[3(y^2+4y)\]
However, carefully looking at the expression, we will notice that this can be factored further. \(y\) can be factored out of the expression in the bracket.
\[3y(?+?)\]
We will go over the process again by dividing the values that y has been factored from by \(y\).
\[\frac{y^2}{y}=y\]
and
\[\frac{4y}{y}=4\]
This leaves us with the final expression in its factored form;
\[3y(y+4)\]
We can evaluate this by expanding the brackets.
\[(3y\times y)+(3y\times 4)=3y^2+12y\]
which again, is what we had at the beginning.
Simplifying Expressions
The term simplifying stems from the root word "simple". As the word suggests, simplifying a given expression allows us to solve them more efficiently. When we simplify an expression, we are reducing it into a simpler form by cancelling Common Factors and regrouping terms that share the same variable.
Simplifying expressions is the process of writing expressions in their most compact and simplest forms such that the value of the original expression is maintained.
This avoids all the lengthy working you might have to perform that may result in unwanted careless mistakes. Surely, you wouldn't want to have any arithmetic errors now, would you?
There are three steps to follow when simplifying expressions.
Eliminate the brackets by multiplying out the factors (if any are present);
Remove exponents by using the exponent rules;
Add and subtract like terms.
Let's go through some worked examples.
Simplify the expression
\[3x+2(x-4).\]
Solution
Here, we will first operate on the brackets by multiplying the factor (outside the bracket) by what is in the brackets.
\[3x+2x-8\]
We will add like terms, which will give us our simplified form as
\[5x-8\]
which indeed holds the same value as the expression we had in the beginning.
Here is another example.
Simplify the expression
\[x(4-x)-x(3-x).\]
Solution
With this problem, we will deal with the brackets first. We will multiply the factors by elements of the brackets.
\[x(4-x)-x(3-x)\]
This yields,
\[4x-x^2-3x+x^2\]
We can go ahead here to rearrange them such that like terms are grouped close together.
\[4x-3x-x^2+x^2\]
Let us now do the additions and subtractions, which will in turn leave us with:
\[4x-3x-x^2+x^2=x\]
Expressions - Key takeaways
- Expressions are mathematical statements that have two terms at least that contain variables, numbers, or both.
- Terms are either numbers or variables or numbers and variables multiplying each other.
- Numerical expressions are a combination of numbers with mathematical operators separating them.
- Factorising is the process of reversing the expansion of brackets.
- The factorising process involves taking out the highest common factors (HCF) from all the terms such that when the factors are taken out and multiplied by the values in the brackets, we will arrive at the same expression we had in the first place.
- Simplifying expressions is the process of writing expressions in their most compact and simplest forms such that the value of the original expression is maintained.
Explanations 
Exams 
Magazine 
