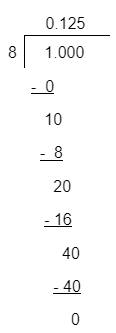Fractions and decimals are two very useful types of rational numbers that you will frequently encounter in Math. They are both used to represent precise values that we are not able to achieve using only whole numbers.
But how can you represent that fraction as a decimal number? Do you know what the relationship between fractions and decimals is?
In this article, we will define what fractions and decimals are. We will show you how to convert fractions to decimals and vice-versa, and how to perform basic operations with them.
Meaning of Fractions and Decimals
First of all, let's define the concepts of fractions and decimals.
Fractions
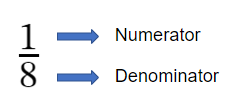
Fractions are numbers that represent parts of a whole. Fractions are written in the form , where and are integers and . The number at the top of the fraction is called the numerator, and the number at the bottom is called the denominator.
The denominator represents the number of parts that the whole is divided into, and the numerator represents how many of those parts you have selected. Let's see this more clearly with an example.
The fraction can be represented as follows,
 Graphical representation of the fraction 1/8, Marilú García De Taylor - StudySmarter Originals
Graphical representation of the fraction 1/8, Marilú García De Taylor - StudySmarter Originals
Let's represent a few more fractions.
Represent the fractions and .
 Graphical representation of the fraction 3/8, Marilú García De Taylor - StudySmarter Originals
Graphical representation of the fraction 3/8, Marilú García De Taylor - StudySmarter Originals
 Graphical representation of the fraction 5/8, Marilú García De Taylor - StudySmarter Originals
Graphical representation of the fraction 5/8, Marilú García De Taylor - StudySmarter Originals
 Graphical representation of the fraction 8/8, Marilú García De Taylor - StudySmarter Originals
Graphical representation of the fraction 8/8, Marilú García De Taylor - StudySmarter OriginalsAll fractions that have the same number in both their numerator and denominator will be equal to one.
Decimals
Decimals are numbers that have a decimal point that separates the whole part from the fractional part of the number.
To be able to understand how decimal numbers work, it is important to grasp the concept of place value. Each number place behaves like a placeholder that can only hold one digit. In the example below, you can see what each number place represents.
The decimal number 342.87 can be represented as follows:
 Place values of a decimal number, Marilú García De Taylor - StudySmarter Originals
Place values of a decimal number, Marilú García De Taylor - StudySmarter Originals
Relationship between Fractions and Decimals
Fractions and decimals are closely related as they are both ways of representing rational numbers and you can convert one into the other. Fractions are written in the form of a division problem. When we go ahead and divide the numerator by the denominator, we obtain the value of the fraction, which is normally a rational number that can be an integer or a decimal, depending on whether the numerator can be exactly divided into the denominator or not.
Another important relation between fractions and decimals that is useful to remember is the following:
a)
b)
c)
a)
b)
c)
Importance of Fractions and Decimals
Fractions and decimals are vital when precise values are required. For example, they are necessary when we are measuring height and length, and also when dealing with money to calculate mortgage payments, salaries, taxes, and the cost of our weekly shop. Fractions and decimals are also used in many fields that require precise calculations like engineering, science, architecture, and economy, among others.
Converting Fractions and Decimals
You can convert fractions into decimals, and vice-versa. Let's see how to proceed in each case.
Converting Fractions into Decimals
Converting fractions into decimal numbers is quite simple – all you need to do is divide the numerator by the denominator. You can do this the easy way using a calculator, or you can use the long division method when working it out by hand.
Write the fraction as a decimal.
Using the long division method:
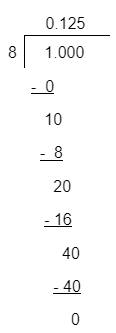
Therefore, the fraction is equal to the decimal number .
When you divide the numerator by the denominator, you might get numbers with non-terminating decimals that repeat in a pattern. For example, In this case, you can use bar notation to represent this type of decimal number. For example, the bar above the decimal 1 means that it repeats forever.
Let's see a few more examples of repeating decimals,
a) so we can write it as
b) in this case, we have two repeating numbers so the bar must cover both decimals:
c) in this example, we have three decimals that repeat in a pattern, so the bar covers the three repeating decimals:
Mixed numbers into decimals
Let's recall the concept of mixed numbers.
Mixed numbers are numbers comprised of two parts, a whole number and a proper fraction. For example, in the mixed number , represents the whole number part, and is the proper fraction.
A proper fraction is a fraction where the number in the numerator is smaller than the number in the denominator .
What happens if you have a mixed number? Can you convert it to decimal too? The answer is yes.
To convert mixed numbers into decimals you need to remember that mixed numbers represent the sum of a whole number and a fraction, so the steps to follow are,
Write the mixed number as the sum of a whole number and a fraction.
Convert the fraction into a decimal number.
Add the whole number to the decimal number calculated in the previous step.
Write the mixed number as a decimal.
Write the mixed number as the sum of the whole number and the fraction.
Convert the fraction into a decimal.
Add the whole number and the decimal.
The mixed number is equivalent to the decimal number .
Converting Decimals into Fractions
To convert decimal numbers into fractions you can follow these steps.
Write the decimal number omitting the decimal point. This will be the numerator of the fraction.
The denominator will be a base 10 number with as many zeros as the number of decimal places in the original decimal number.
Simplify the resulting fraction to its simplest form.
a) Write the decimal number 4.50 as a fraction.
450 will be the numerator.
4.50 has two decimal places, so the denominator will be 100.
The resulting fraction is .
Now we need to simplify the fraction to its simplest form,
The decimal number 4.50 is equal to the fraction .
b) Write the decimal number 1.8 as a fraction.
18 will be the numerator.
1.8 has one decimal place, so the denominator will be 10.
The resulting fraction is .
Now we simplify the fraction to its simplest form,
The decimal number 1.8 is equal to the fraction .
c) Write the decimal number 4.225 as a fraction.
4225 will be the numerator.
4.225 has three decimal places, so in this case, the denominator is 1000.
The resulting fraction is
Simplifying the fraction to its simplest form,
The decimal number 4.225 is equal to the fraction .
How to Simplify Fractions and Decimals
In the previous examples, we simplified the fraction into its simplest form. What exactly does that mean?
A fraction is in its simplest form if its numerator and denominator have no other common factors besides 1. This means that both the numerator and the denominator cannot be any smaller, they can only be divided by 1, while remaining as whole numbers.
Let's explain in more detail how to achieve this. The process to simplify fractions is as follows.
Divide the numerator and denominator by the greatest number that divides them both exactly. The result of both divisions must be a whole number.
Repeat step 1 until the fraction is in its simplest form.
Simplify the fraction to its simplest form.
Divide numerator and denominator by 8, as 120 and 48 are both divisible by 8
Divide numerator and denominator by 3.
The resulting fraction is in its simplest form, because its numerator and denominator have no other common factors besides 1.
Another special case that you might encounter is when you have a fraction that contains a decimal number as numerator or denominator, in this case, you can simplify it as follows.
Convert the decimal number into a fraction. This will produce a fraction into a fraction.
Divide the numerator by the denominator, which in this case, is the same as multiplying the numerator by the reciprocal of the denominator.
Simplify the resulting fraction to its simplest form.
Simplify the fraction
Convert the decimal into a fraction.
Multiply the numerator by the reciprocal of the denominator (The reciprocal of 2 is ).
Simplify the fraction to its simplest form by dividing the numerator and denominator by 4, since 8 and 20 are both dividable by 4.
Addition and Subtraction of Decimals and Fractions
To add and subtract decimals and fractions you can proceed in two alternative ways,
Using decimals: convert the fraction to a decimal number, and then add or subtract the decimal numbers together.
Using fractions: convert the decimal number into a fraction, and then add or subtract the fractions together. After that, simplify the resulting fraction to its simplest form.
a) Add
Using decimals,
Using fractions,
1.25 converted into a fraction equals .
Simplify the fraction to its simplest form.
b) Subtract .
Using decimals,
.
Using fractions,
0.25 converted into a fraction equals .
Simplify the fraction to its simplest form.
How to Multiply Decimals and Fractions
To multiply decimals and fractions you can follow the same two alternative ways that you use to add and subtract them.
Using decimals: convert the fraction to a decimal number, and then multiply the decimal numbers together.
Using fractions: convert the decimal number into a fraction, and then multiply the numerators and the denominators of the fractions together. After that, simplify the resulting fraction to its simplest form.
Multiply
1. Using decimals,
Convert the fraction to a decimal
Then you can use a calculator to multiply , or work it out by hand, as follows,
- Multiply as you would normally, but ignore the decimal points.
- To work out the number of decimal places of the answer, you need to add the decimal places of the two numbers being multiplied.
1.5 has 1 decimal place, and 0.25 has 2 decimal places, so the answer will have 3 decimal places:
2. Using fractions:
Convert the decimal number into a fraction.
Multiply the numerators and the denominators of the fractions together.
The fraction is already in its simplest form, since 3 and 8 have no common divisors, apart from 1.
Solving Linear Equations with Fractions and Decimals
To solve linear equations with fractions and decimals you can follow the same rules that you use to solve equations with integers.
Let's see some examples below.
a) Solve
Add 1.5 to both sides of the equation to isolate x
b) Solve
Subtract from both sides of the equation to isolate x
Because the
denominators are different, you need to make a common denominator using the
Lowest Common Denominator (LCD), which is 6. So, to get 6 as a common denominator you need to multiply the first fraction by 2 (top and bottom), and the second fraction by 3 (also top and bottom).
c) Solve
Multiply both sides of the equation by 4 to isolate x (4 is the reciprocal of )
Fractions and decimals - Key takeaways
- Fractions are numbers that represent parts of a whole. Fractions are written in the form , where a and b are integers and .
- Decimals are numbers that have a decimal point that separates the whole part from the fractional part of the number.
- Fractions and decimals are closely related as they are both ways of representing rational numbers, and you can convert one into the other.
- Fractions and decimals are vital when precise values are required.
- A fraction is in its simplest form if its numerator and denominator have no other common factors besides 1.
- To add, subtract, and multiply decimals and fractions you can proceed in two alternative ways: using decimals or using fractions.
- To solve linear equations with fractions and decimals you can follow the same rules that you use to solve equations with integers.