What is an example of a logarithm base function?

An example of a logarithm base function is: y = log 2 X.

What are the four laws of logarithm?

The four laws of logarithm are: log b (x) + log b (y) = log b (x y) (product law) log b (x) - log b (y) = log b (x/y) (division law) log b (x n ) = n log b (x) (power law) log b (x) = log a (x) / log a (b) (change of base law)

Logarithm Base

TABLE OF CONTENTS :

TABLE OF CONTENTS

Lerne mit deinen Freunden und bleibe auf dem richtigen Kurs mit deinen persönlichen Lernstatistiken

Jetzt kostenlos anmelden

Nie wieder prokastinieren mit unseren Lernerinnerungen.

Jetzt kostenlos anmelden

Logarithm is an exponent that defines how many times a number can be multiplied to get another number. It is the power to which a number (the base) is raised to get another number. When talking about logarithms, there are terms you need to remember and be able to identify like the exponent and the base.

We are going to focus more on the bases of logarithms. Hence, we should be able to identify a base when we see it. Let's get familiar with the basic formula associated with logarithms and then identify the base.

$b^{y} = X$

b is the base, y is the exponent to which the base is raised and X is the result obtained.

It is also written as: $\log_{b} (X) = y$

where log is short for logarithm.

If you have $2^{3} = 8$ , 2 is the base, 3 is the exponent and 8 is the result obtained. It can also be written as $\log_{2} 8 = 3$ . If we are able to identify the base in a logarithmic expression, we can deduce the meaning of a base.

Logarithm base meaning

Logarithm base is the subscript of the logarithm symbol (log). You can say that it is the number that carries or raises the exponent depending on the form of the expression ( $b^{y} = X$ or $\log_{b} (X) = y$ ). Let's take some examples to strengthen our understanding on identifying a base.

Identify the base in the following.

$\log_{3} 9 = 2$
$5^{4} = 625$

Solution

The base here is 3. It is the subscript of the logarithm symbol log.
The base here is 5. It is the number that raises the exponent 4.

The popular forms of logarithms are the common logarithm and natural logarithm. The common logarithm is in base 10 written as $\log_{10}$ or just $\log$ and the natural logarithm is in base e written as $\log_{e}$ or $\ln$ . When solving common logarithms with base 10, it's best to use a calculator. The calculator has a log button that will give you the answer. You can try to do it without a calculator if the numbers are small and easy to calculate but if otherwise, reach out for your calculator.

Give the answers to the following.

$\log (1000)$
$\log (20)$
$\log (8)$

SolutionWe can see that the questions are all in base 10.a. You can get the answer to

\log (1000)

using your calculator. Just press the log button and type in 1000 you will get the answer.

\log 1000 = 3

This means that if you multiplying 10 in three places gives 1000 that is $10^{3}$ .

It is also possible to do this without a calculator because we can calculate that

10^{3}

= 1000.b. log 20 = 1.3010c. log 8 = 0.9031

For the natural logarithm in base e, the e is called Euler's number which is 2.71828. When you want to solve this, you use the $\ln$ button in your calculator to get the answer.

Let's see some more examples.

Give the answers to the following

a. $\log_{e} 7.3$

b. $\ln (25)$

c. $\log_{e} 33.98$

Solution

To get the answer to $\log_{e} 7.3$ , you'll need a calculator. You will need to press the $\ln$ button on the calculator and then 7.3. The answer will appear after that.

$\log_{e} 7.3 = 1.9878$

b. Using a calculator, $\ln (25) = 3.2188$

c. Using a calculator, $\log_{e} (33.98) = 3.5257$

Aside from the common logarithm and natural logarithm with bases 10 and e, logarithms can also have any base. The base can be any number. For example $\log_{7} (56)$ , $\log_{2} (4) + \log_{6} (8)$ and $\log (100) - \log_{2} (10)$ are logarithms with different bases.

Solving logarithms with different bases

When you have logarithms with different bases, it means that you have a logarithmic equation or expression where the bases are of different numbers. The way to go about this is to use a formula called the change of base formula. The aim here is to make the different bases equal. That way, you will be able to get a solution easily. Let's take a look at what the change of base formula looks like.

$\log_{b} (x) = \frac{\log_{a} (x)}{\log_{a} (b)}$

The logarithmic rules we would normally use are the same rules for solving logarithmic base. Let's see some of those rules.

$\log_{b} (x) + \log_{b} (y) = \log_{b} (x y)$
$\log_{b} (x) - \log_{b} (y) = \log_{b} (\frac{x}{y})$
$\log_{b} (x^{n}) = n \log_{b} (x)$
$\log_{b} (x) = \log_{b} (y) \Leftrightarrow x = y$

We need these formulas to help us because our calculators can only solve logarithms in base "10" and base "e". Let's see how the change of base formula is used in the following examples.

Simplify $y = \log_{2} (20)$

Solution

The first thing is to change the base using the change of base formula. You can change the base to any number including base 10 and the natural logarithm e. You just have to make sure that they are both the same base. Doing this we will have:

$\log_{2} (20) = \frac{\log_{10} (20)}{\log_{10} (2)}$

We will use a calculator to solve the numerator and denominator to get:

$\frac{\log_{10} (20)}{\log_{10} (2)} = \frac{1.3010}{0.3010} = 4.32$

Let's see more examples.

Solve $\log_{3} (x) = \log_{9} (4)$

Solution

You will notice that there are different bases involved so we will use the change of base formula. We can change both base to 3 or 9 and you will still arrive at the same answer. Remember the aim is just to make sure that both bases are equal.

We will use the change of base formula on the right hand side. This means we are making the bases 3.

$\log_{3} (x) = \frac{\log_{3} (4)}{\log_{3} (9)} \log_{3} (x) = \frac{\log_{3} (4)}{\log_{3} (3^{2})}$

There is a logarithm law in the form $\log_{b} (b^{n}) = n$ . We will apply this law to the denominator present and we will have:

$\log_{b} (b^{n}) = n \log_{3} {(3)}^{2} = 2$

We will put the result "2" in the equation and continue solving.

$\log_{3} (x) = \frac{\log_{3} (4)}{2} \log_{3} (x) = \frac{1}{2} \log_{3} (4)$

There is another logarithm law in the form $\log_{a} (x^{n}) = n \log_{a} (x)$ . If we apply this we will get:

$\log_{3} (x) = \log_{3} (4^{\frac{1}{2}}) \log_{3} (x) = \log_{3} (2)$

Using the rule that if $\log_{b} (x) = \log_{b} (y)$ , then $x = y$ , our final answer will be:

$x = 2$

Solve $\log_{9} (4) + \log_{3} (x) = 3$

Solution

The first thing is to make the bases the same. We can choose to make them both 9 or 3. Either way, we will arrive at the same answer. Let's make them both 3.

The change of base formula is: $\log_{b} (x) = \frac{\log_{a} (x)}{\log_{a} (b)}$

We will use the change of base formula on the first term of the expression and we will get:

$\frac{\log_{3} (4)}{\log_{3} (9)} + \log_{3} (x) = 3$

If you observe, you will see that you can simplify the denominator with a calculator or manually. You can tell that the result is 2 because 3 squared is 9. So, we will now have:

$\frac{\log_{3} (4)}{2} + \log_{3} (x) = 3$

Let's multiply each term by 2

$\log_{3} (4) + 2 \log_{3} (x) = 6$

We can use the power logarithmic rule on the second expression which is $\log_{b} (x^{n}) = n \log_{b} (x)$

We will now have $\log_{3} (4) + \log_{3} (x^{2}) = 6$

We can use the addition rule here which is $\log_{b} (x) + \log_{b} (y) = \log_{b} (x y)$

Therefore $\log_{3} (4 x^{2}) = 6$

We will now take the anti log to get

$4 x^{2} = 3^{6}$

What we simplify did here was to raise the base 3 to the power of 6.

The next and final step is to find x

$x^{2} = \frac{3^{6}}{4}$

Take the square root of both sides

$\sqrt{x^{2}} = \sqrt{\frac{3^{6}}{4}} \sqrt{x^{2}} = \frac{27}{2} x = \frac{27}{2} = 13.5$

Logarithms are sometimes expressed in a graphical form and the base of the logarithmic function can affect the outcome of the graph. What happens is that the bigger the base, the smaller the curve. In other words, the larger the base, the closer the curve gets to the y-axis.

Let's take an example

Plot the logarithmic expressions and observe the plot.

$y = \log_{2} (x)$ and $y = \log_{10} (x)$

Solution

What you need to do is make a table for both expressions and plot the graph.

For $y = \log_{2} (x)$

x	y
1	0
2	1
4	2

For $y = \log_{10} (x)$

x	y
1	0
2	0.3
4	0.6

We will now plot the graph

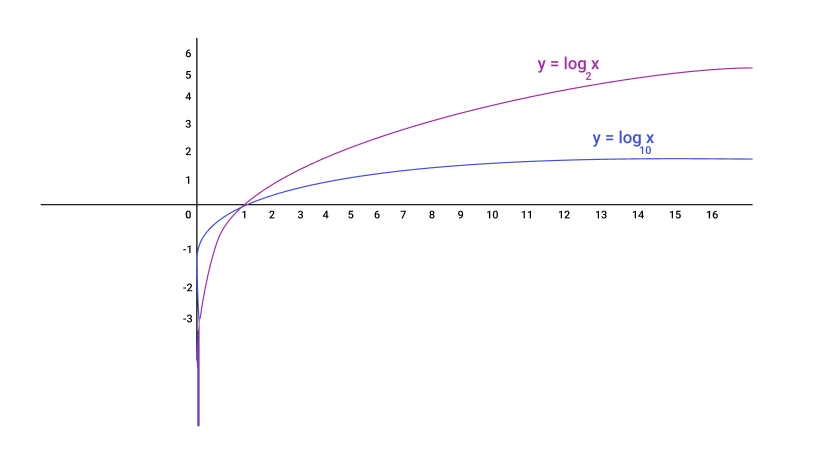
Bases of Logarithms Logarithm graphs StudySmarter

You can see that $y = \log_{10} (x)$ is closer to the y axis.

Bases of Logarithms - Key takeaways

Logarithm base is either the subscript of the logarithm symbol (log) or the number that carries or raises the exponent depending on the from of the expression ( $b^{y} = X$ or $\log_{b} (X) = y$ ).
To solve logarithms with different bases, you use the change of base formula which is $\log_{b} (x) = \frac{\log_{a} (x)}{\log_{a} (b)}$
The bigger the logarithm base, the smaller the curve on the graph. In other words, the larger the base, the closer the curve gets to the y-axis.

Frequently Asked Questions about Logarithm Base

To find the base of a logarithm, you should be able to identify the base. The base is usually the subscript of the logarithm symbol (log). For example, the base in log₂4 is 2.

An example of a logarithm base function is:

y = log₂ X.

The four laws of logarithm are:

log_b(x) + log_b(y) = log_b(x y) (product law)
log_b(x) - log_b(y) = log_b(x/y) (division law)
log_b(xⁿ) = n log_b(x) (power law)
log_b(x) = log_a(x) / log_a(b) (change of base law)

The larger the base, the closer the curve gets to the y-axis. The larger the base, the smaller the curve.

Logarithm base is either the subscript of the logarithm symbol (log) or the number that carries or raises the exponent depending on the from of the expression (b^y = X or log_a(X) =y).

Flashcards in Logarithm Base20 Start learning

What is a natural logarithm function?

A logarithm function with base e.

What is a natural base exponential function?

An exponential function with base e.

"The natural logarithmic function is the inverse of the natural base exponential function"

Is the statement above true or false?

True.

Express the natural logarithm as a function of y.

$y = \ln x$.

Express the natural base exponential as a function of y.

$y = e^x$.

What do you call the constant e in the natural logarithm? Write the value of e correct to 3 decimal places.

The Napier constant, e = 2.718

Learn with 20 Logarithm Base flashcards in the free StudySmarter app

Already have an account? Log in

More about Logarithm Base

Save Article

How would you like to learn this content?

Creating flashcards

Studying with content from your peer

Taking a short quiz

How would you like to learn this content?

Creating flashcards

Studying with content from your peer

Taking a short quiz

Free math cheat sheet!

Everything you need to know on . A perfect summary so you can easily remember everything.

Email Address*

Find Study Materials for

Create Study Materials

Logarithm Base

Logarithm base meaning

Solving logarithms with different bases

Bases of Logarithms - Key takeaways

Frequently Asked Questions about Logarithm Base

Join over 22 million students in learning with our StudySmarter App

This is still free to read, it's not a paywall.

You need to register to keep reading

This is still free to read, it's not a paywall.

You need to register to keep reading

Entdecke Lernmaterial in der StudySmarter-App

Logarithm Base

Logarithm base meaning

Solving logarithms with different bases

Bases of Logarithms - Key takeaways

Frequently Asked Questions about Logarithm Base

How do you find the base of a logarithm?

What is an example of a logarithm base function?

What are the four laws of logarithm?

How does the base of logarithm function affect a graph?

What is the meaning of logarithm base?

Learn with 20 Logarithm Base flashcards in the free StudySmarter app

Join over 22 million students in learning with our StudySmarter App

This is still free to read, it's not a paywall.

You need to register to keep reading

This is still free to read, it's not a paywall.

You need to register to keep reading

Create a free account to save this explanation.

Entdecke Lernmaterial in der StudySmarter-App

Join over 22 million students in learning with our StudySmarter App

Join over 22 million students in learning with our StudySmarter App