Lowest Common Denominator

TABLE OF CONTENTS :

TABLE OF CONTENTS

Lerne mit deinen Freunden und bleibe auf dem richtigen Kurs mit deinen persönlichen Lernstatistiken

Nie wieder prokastinieren mit unseren Lernerinnerungen.

Imagine you are having a Thanksgiving dinner, and everyone decides to contribute a fraction of their pizza to you. Can you determine how much pizza is in your possession? In order to achieve this, the concept of the lowest common denominator must be understood. Hereafter, you shall be learning this.

This article will explore the definition of the lowest common denominator, and examples of the application of this concept.

What is the Lowest Common Denominator?

Given a list of fractions, the lowest common denominator (LCD) is the smallest multiple that is common to the denominators of the fractions. It is often referred to as the Lowest Common Multiple (LCM) of denominators.

This sounds complicated, but it's really not. Let's have a look at an example:

The Lowest Common Denominator of $ \frac{2}{3}$ and $ \frac{3}{4}$ is $12$, since $12$ is a multiple of both the denominators $(3$ and $4),$ and it's the smallest multiple of these numbers you can find.

When a list of fractions is given, and the LCD is to be determined, we look for the lowest number large enough to be divided by each denominator of the list without a remainder.

What is a Common Denominator?

A common denominator is a number that can be divided by other denominators without a remainder. This number is a multiple of other denominators.

You consider the fractions $\frac{3}{4}$ and $\frac{5}{6}$ : their common denominator must be divisible by both denominators (4 and 6) without a remainder. Thus, in order to find their common denominator, you have to consider multiples of each denominator.

Multiples of 4 are: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, ...

Multiples of 6 are: 6, 12, 18, 24, 30, 36, 42, ...

Amongst the multiples of both denominators listed above, the common multiples are 12, 24, 36… This is true because when these numbers are divided by the denominators 4 and 6, they do not have a remainder.

However, the multiples of a number are infinite. Imagine how many numbers would be written as multiples of 4 and 6, we probably would run out of papers. So, mathematicians came up with the lowest common denominator or lowest common multiple, which uses only the smallest number which is a multiple among a set of numbers.

Hence, the LCD between 4 and 6 is 12.

How to Find the Lowest Common Denominator?

There are four methods that can be used in finding the LCD:

LCD rules
Multiples' listing
Prime factor product
Combined prime factor product.

Simple rules to find LCD

One way to solve either LCM or LCD is by applying the LCD rules. Note that these rules are best applied only among a set of two numbers. It can also be used in a list of numbers above two but may be more complex if not well applied.

The following are the LCD rules:

Equal denominators

When two fractions have the same denominator, the LCD is that denominator.

One denominator rules them all

If a number among a set of denominators is a multiple of all other numbers in that set, the LCM is that multiple.

Prime denominators

The LCD of a set of denominators which are prime numbers is the product of those prime numbers. You must ensure that these denominators are prime numbers.

No common factors

The LCD of a list of denominators that have no common factor is the product of those denominators. You must be sure that no number can divide any pair without a remainder.

The tricky one with a common factor

If there is a common factor between a set of two numbers, the LCD is obtained by the following two steps:

Divide one of the two numbers by their highest common factor to get the first result.
Multiply your first result with the other number. This answer becomes the LCD.

Examples of Lowest Common Denominator Rules

Equal denominators - example

For instance, the LCD between fractions $\frac{3}{2}$ and $\frac{1}{2}$ is 2 because the denominator of the fractions is the same.

One denominator rules them all - example

The LCD between $\frac{3}{4}$ , $\frac{1}{2}$ , and $\frac{3}{20}$ is 20. This is because, in the denominators list of 2, 4 and 20, we have that 2 and 4 are factors of 20. Thus, 20 is a multiple of 2 and 4, so, 20 is the LCD.

Prime denominators - example

The LCD between $\frac{2}{3}$ and $\frac{1}{5}$ is 15. These denominators 3 and 5 are prime numbers. Thus,

$3 \times 5 = 15$

15 is the LCD here.

No common factors - example

The LCD between $\frac{7}{9}$ and $\frac{3}{10}$ is 90. Denominators 9 and 10 are not prime numbers. Most importantly, there is no common factor between these two numbers. So the LCD is

$9 \times 10 = 90$

The tricky one with a common factor - example

The LCD between $\frac{3}{8}$ and $\frac{7}{20}$ is 40. The highest common factor between 8 and 20 is 4. Divide 8 by 4 and your first answer is 2. Then multiply your first result which is two by the other number 20,

$2 \times 20 = 40$

So the LCD, in this case, is 40.

In some scenarios, you may not be able to understand which LCD rule you should apply. In these cases, the following methods to find the lowest common denominator of a list of fractions come in handy.

Multiples' listing method

In this method, you are to list some multiples of each denominator. Afterward, you pick the lowest common multiple among all multiples listed - that is the left-most number that appears in both lists. To apply this method, you should be familiar with the multiplication table

Find the LCD of $\frac{1}{2}$ , $\frac{3}{4}$ and $\frac{5}{6}$ .

Solution:

Step 1. What are the denominators?

The denominators are 2, 4 and 6

Step 2. Write out the multiple of these numbers.

Multiples of 2 are 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, ...

Multiples of 4 are 0, 4, 8, 12, 16, 20, 24 , 28, 32, 36, 40, 44, 48, ...

Multiples of 6 are 0, 6, 12, 18, 24 , 30, 36, 42, 48, 54, 60, 66, 72, ...

You would notice that 12 and 24 are common multiples of 2, 4 and 6. But, we want the lowest common multiple. So, our lowest common multiple is 12. This means that our LCD is 12 .

When you should use the multiples' listing method

Note that the Multiples' listing method is best used when

The numbers involved are small, something between 2 to 12 eg, 2, 3, 4, 5, 6, 7... 12. Above 12 it gets tricky to write multiples down!
There are no more than 3 fractions.

More technically, the number of elements in a set is called the cardinality of the set. So the listing method is best applied on sets of fractions with cardinality 3 or less.

E.g, finding the LCD between $\frac{2}{5}$ and $\frac{2}{7}$ or between $\frac{1}{2}$ , $\frac{1}{3}$ and $\frac{3}{4}$ . This would reduce mistakes and time spent in finding the LCD.

Find the LCD between $\frac{2}{5}$ and $\frac{2}{7}$

Solution:

Step 1. What are the denominators?

The denominators are 5 and 7

Step 2. Write out the multiple of these numbers.

Multiples of 5 are 0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, ...

Multiples of 7 are 0, 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, ...

From the above, it is clear that the LCD is 35.

Find the LCD between $\frac{1}{2}$ , $\frac{1}{3}$ and $\frac{3}{4}$ .

Solution:

Step 1. What are the denominators?

The denominators are 2, 3 and 4

Step 2. Write out the multiple of these numbers.

Multiples of 2 are 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, ...

Multiples of 3 are 0, 3, 6, 9, 12, 15, 18, 21, 24 , 27, 30, 33, 36, ...

Multiples of 4 are 0, 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, ...

You would notice that 12 and 24 are common multiples of 2, 4 and 6. But, we want the lowest common multiple. So, our lowest common multiple is 12. This means that our LCD is 12.

3. The difference between any two numbers in a list is not more than 10.

All these must be considered before applying this method because it helps you stay within the range of your multiplication table.

Prime factor product method

The prime factor product method is done by writing each number of a set as a product of its prime factors. Remember that a prime factor is a prime number that divides another number without a remainder.

Find the LCD between $\frac{11}{24}$ and $\frac{7}{10} .$

Solution:

Step 1: Write out the denominators.

The denominators are; 24 and 10.

Step 2: Express each denominator as a product of its prime factor. To achieve this, you have to follow some simple sub-steps.

Sub-step A: Draw a column table with the denominator in the second column.

	24

Sub-step B: Use the smallest factor of the denominator and divide the number gradually until you arrive at 1. Remember that the factor is written in the first column.

2	24
	12

2	24
2	12
	6

2	24
2	12
2	6
	3

2	24
2	12
2	6
3	3
	1

Sub-step C: Write all factors in the first column as a product.

2	24
2	12
2	6
3	3
	1

Repeat the same step for the other denominator and you would have:

2	10
5	5
	1

Step 3: Arrange these prime factors being multiplied and circle out similar factors.

Lowest Common Denominator Third step in the prime factor method of finding the LCD StudySmarter Third step in the prime factor method of finding the LCD, StudySmarter Originals

This means that the common factor between 24 and 10 is 2.

Step 4: Multiply the rest of the factors which are not circled with your common factor.

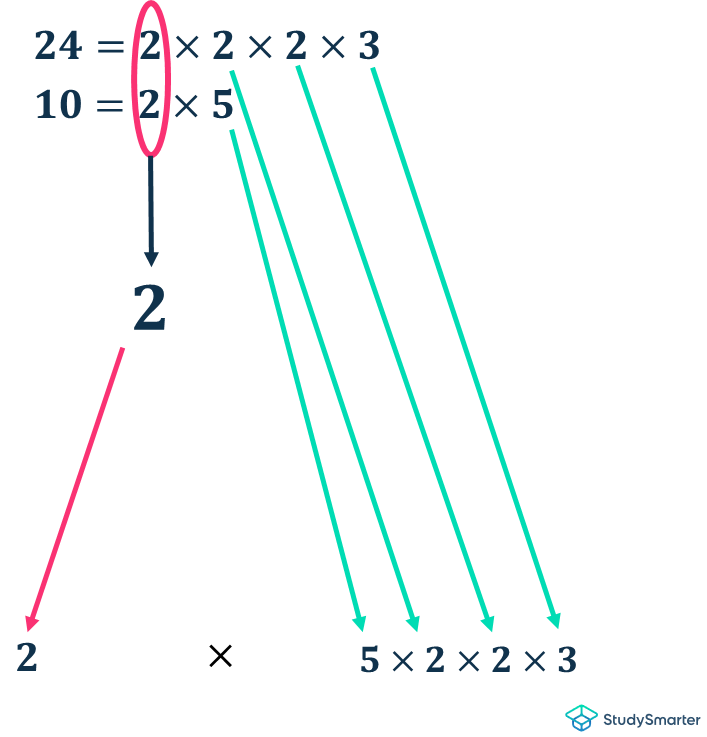
Lowest Common Denominator Fourth step in the prime factor method of finding the LCD StudySmarter

Fourth step in the prime factor method of finding the LCD, StudySmarter Originals

So, our LCD is;

$2 \times 5 \times 2 \times 2 \times 3 = 120$

Combined prime factor product method

As a variation on the Prime Factor Product Method, the Combined Prime Factor Product Method requires that you find the prime factors of the denominators in just a single table. Once you are familiar with the technique, this method has the advantage of being more concise.

Find the LCD between $\frac{11}{24}$ and $\frac{7}{10} .$

Solution:

Step 1. Write out the denominators.

The denominators are 24 and 10.

Step 2. Create a table with the number of columns according to the number of denominators. In this case, the number of columns is 3 (one more than the number of denominators). Leave the first column for the factors.

	24	10

Step 3. Use the smallest prime factor to divide the denominators. Note that a factor may only be able to divide one denominator but fail to divide the rest. In such cases where the factor cannot divide one of the numbers in the denominator column, just write the same number in the cell below. You just need that factor to divide at least one of the denominators. It is easier by firstly trying out the smaller numbers like, 2,3, ... Remember that the factor is written in the first column.

2	24	10
	12	5

Note that in this case 2 can divide both 24 and 10 without a remainder.

2	24	10
2	12	5
	6	5

Note that 2 can divide 12 but cannot divide 5, so we still bring down 5 in the cell below.

2	24	10
2	12	5
2	6	5
	3	5

2	24	10
2	12	5
2	6	5
3	3	5
	1	5

2	24	10
2	12	5
2	6	5
3	3	5
5	1	5
	1	1

Step 4: Write all factors in the first column as a product.

2	24	10
2	12	5
2	6	5
3	3	5
5	1	5
	1	1

Once you are left with ones in the last row, you can calculate the LCD as the product of the factors in the first column.

The LCD between the denominators 24 and 10 is then

$2 \times 2 \times 2 \times 3 \times 5 = 120$

The combined prime factor product method is the best method for a large set of denominators.

Applications of LCD

As mentioned earlier, the lowest common denominator is used in simplifying fractions involving addition and subtraction. Also, it is also used to arrange fractions in ascending and descending order. Let us take some examples to best understand its applications.

LCD in fractions

Simplify

$\frac{1}{2} - \frac{1}{4}$

Solution:

Step 1. Find the LCD of the denominators.

Using the LCD rules method, the 2^nd rule says that if one of the denominators is a multiple of the other denominators, then the LCD is such multiple.4 is a multiple of 2, so the LCD between 2 and 4 is 4.Step 2. Use the LCD as a general denominator. Then divide the LCD by each denominator and multiply by the numerator.

$\frac{1}{2} - \frac{1}{4} = \frac{1 \times (4 \div 2) - 1 \times (4 \div 4)}{4}$

Step 3. Solve the arithmetic.

$\frac{1 \times (2) - 1 \times (1)}{4} = = \frac{2 - 1}{4} = \frac{1}{4}$

Simplify

$\frac{3}{5} + \frac{5}{7} + \frac{1}{28}$

Solution:

Step 1: Find the LCD of the denominators.

Use the combined prime factor product method.

2	5	7	28
2	5	7	14
5	5	7	7
7	1	7	7
	1	1	1

The LCD of $\frac{3}{5}$ , $\frac{5}{7}$ and $\frac{1}{28}$ is the product of the numbers in the first column, that is

$2 \times 2 \times 5 \times 7 = 140$ .

Step 2: Use the LCD as a general denominator. Then divide the LCD by each denominator and multiply by the numerator.

$\frac{3}{5} + \frac{5}{7} + \frac{1}{28} = \frac{3 \times (140 \div 5) + 5 \times (140 \div 7) + 1 \times (140 \div 28)}{140}$

Step 3: Solve the arithmetic.

$\frac{3 \times (28) + 5 \times (20) + 1 \times (5)}{140} = = \frac{84 + 100 + 5}{140} = \frac{189}{140}$

Step 4: See if any number can divide through the numerator and denominator to simplify your fraction.

Divide the numerator and denominator by 7

id="3047903" role="math" $\frac{189 \div 7}{140 \div 7} = \frac{27}{20} = 1 \frac{7}{20}$

LCD in Comparing fractions

With the application of LCD fractions can now be compared to find out which fractions are larger or smaller. It is on this knowledge that fractions can either be arranged in ascending or descending order.

Arrange the following fractions in descending order:

\frac{2}{5}' \frac{1}{6}, \frac{3}{20}

and

\frac{1}{8}

Solution:In arranging fractions in descending order, you are expected to write the fractions from the biggest to the smallest.Step 1. Find the LCD of the given fractions.Using the combined prime factor method, we have;

2	6	20	8	5
2	3	10	4	5
2	3	5	2	5
3	3	5	1	5
5	1	5	1	5
	1	1	1	1

The LCD of denominators 6, 20, 8 and 5 is

$2 \times 2 \times 2 \times 3 \times 5 = 120$ .

Step 2: Use the LCD as a general denominator. Then divide the LCD by each denominator and multiply by the numerator separately.

$\frac{1}{6} = \frac{1 \times (120 \div 6)}{120} = \frac{1 \times (20)}{120} = \frac{20}{120} \frac{3}{20} = \frac{3 \times (120 \div 20)}{120} = \frac{3 \times (6)}{120} = \frac{18}{120} \frac{1}{8} = \frac{1 \times (120 \div 8)}{120} = \frac{1 \times (15)}{120} = \frac{15}{120} \frac{2}{5} = \frac{2 \times (120 \div 5)}{120} = \frac{2 \times (24)}{120} = \frac{48}{120}$

Step 3: Only use the numerators in bold. Now arrange them from highest to lowest.

48, 20, 18 and 15 which is

$\frac{2}{5}' \frac{1}{6}, \frac{3}{20}$ and $\frac{1}{8}$

Lowest Common Denominator - Key takeaways

The lowest common denominator (LCD) is the smallest multiple that is common between a set of denominators.
There are four methods that can be used in finding the LCD; LCD rules, multiples' listing, prime factor product, and combined prime factor product.
LCD is applied when adding and subtracting fractions. Similarly, it is used in arranging fractions in ascending or descending orders.

Frequently Asked Questions about Lowest Common Denominator

The lowest common denominator (LCD) is the smallest multiple that is common between a set of numbers or denominators.

There are four methods which can be used in finding the lowest common denominator; LCD rules, multiples' listing, prime factor product and combined prime factor product.

An example of the lowest common denominator (LCD) is if you are asked the LCD between the denominators 2, 3 and 5. The LCD is 30 because 30 is the smallest multiple that is divisible by these numbers without a remainder.

Lowest common denominator is practically used in adding and substracting fractions. Also, it is used in arranging fractions in either ascending or descending order.

The LCD rules help you find the LCD in a quicker way and there are basically 5 of them.

Flashcards in Lowest Common Denominator7 Start learning

What is a common denominator?

A common denominator is a number which can be divided by other denominators without a remainder.

What is the LCD between half and a quarter?

What is the LCD between one-third and one-fifth?

If 5, 8, 6 and 15 are respective denominators of fractions, what is their LCD?

120

What are the prime numbers in the between 5 and 20?

7, 11, 13, 17 and 19.

What are the factors of 24?

2, 3, 4, 6, 8, 12 and 24

Learn with 7 Lowest Common Denominator flashcards in the free StudySmarter app

Already have an account? Log in

More about Lowest Common Denominator

Save Article

How would you like to learn this content?

Creating flashcards

Studying with content from your peer

Taking a short quiz

How would you like to learn this content?

Creating flashcards

Studying with content from your peer

Taking a short quiz

Free math cheat sheet!

Everything you need to know on . A perfect summary so you can easily remember everything.

Email Address*

Find Study Materials for

Create Study Materials

Lowest Common Denominator

What is the Lowest Common Denominator?

What is a Common Denominator?

How to Find the Lowest Common Denominator?

Simple rules to find LCD

Equal denominators

One denominator rules them all

Prime denominators

No common factors

The tricky one with a common factor

Examples of Lowest Common Denominator Rules

Equal denominators - example

One denominator rules them all - example

Prime denominators - example

No common factors - example

The tricky one with a common factor - example

Multiples' listing method

When you should use the multiples' listing method

Prime factor product method

Combined prime factor product method

Applications of LCD

LCD in fractions

LCD in Comparing fractions

Lowest Common Denominator - Key takeaways

Frequently Asked Questions about Lowest Common Denominator

Join over 22 million students in learning with our StudySmarter App

This is still free to read, it's not a paywall.

You need to register to keep reading

This is still free to read, it's not a paywall.

You need to register to keep reading

Entdecke Lernmaterial in der StudySmarter-App

Lowest Common Denominator

What is the Lowest Common Denominator?

What is a Common Denominator?

How to Find the Lowest Common Denominator?

Simple rules to find LCD

Equal denominators

One denominator rules them all

Prime denominators

No common factors

The tricky one with a common factor

Examples of Lowest Common Denominator Rules

Equal denominators - example

One denominator rules them all - example

Prime denominators - example

No common factors - example

The tricky one with a common factor - example

Multiples' listing method

When you should use the multiples' listing method

Prime factor product method

Combined prime factor product method

Applications of LCD

LCD in fractions

LCD in Comparing fractions

Lowest Common Denominator - Key takeaways

Frequently Asked Questions about Lowest Common Denominator

What is the lowest common denominator?

How do one find the lowest common denominator?

What is an example of lowest common denominator?

What are the practical usage of lowest common denominator?

What are the rules in LCD?

Learn with 7 Lowest Common Denominator flashcards in the free StudySmarter app

Join over 22 million students in learning with our StudySmarter App

This is still free to read, it's not a paywall.

You need to register to keep reading

This is still free to read, it's not a paywall.

You need to register to keep reading

Create a free account to save this explanation.

Entdecke Lernmaterial in der StudySmarter-App

Join over 22 million students in learning with our StudySmarter App

Join over 22 million students in learning with our StudySmarter App