Everything around us comprises geometrical shapes. The geometrically best description of how Berlin can be represented in a globe is a point!
We come across many types of lines in roads, edges of the wall, doors, and so on. The surface of the movie screen is two-dimensional and it resembles a plane.
Here, we will see the introduction for points, lines, and planes.
Identifying points, lines and planes
A point is an exact location in space. A point does not have width, length, or height and so they do not have any dimension.
Points are used to represent a particular location in diagrams and graphs. They are usually labeled in capital letters. In the diagram below, we have three points and they are labelled A, B, and C.
Points, StudySmarter Original
Lines are formed by infinite points that extend on both sides.
Unlike points, lines have length and so they are one-dimensional objects, that extend on both sides infinitely.
If there are two points A and B on the line we can represent a line by writing it as or .
Usually, when there are no points on a line it is represented by script letters, such as r, s, and t.
A line which has a start point but no endpoint is called a ray.
The ray containing two points A and B, with A as the starting point is represented by .
A line which has both a start and end points is called a line segment.
The segment between the points A and B is written as .
Ray, line segment and line, StudySmarter OriginalPlanes can be thought of as infinitely many intersecting lines that extend forever in all directions.
Planes can have both length and width and so are two-dimensional objects. Planes are also represented by capital letters.
Plane, StudySmarter Original
Types of points
In this subsection, we will learn about collinear, non-collinear, coplanar, non-coplanar points, and point of concurrency.
Given a point, we can draw an infinite number of lines that passes through that point. However, there is exactly only one line that can be drawn that passes through two given points.
In the diagram below, the only line that could be drawn through 2 points P and Q is given.
Only one line through points P and Q, StudySmarter Original
Suppose now we have 3 or more points, then we ask the question: does there exists a line which passes through all the given points? Depending on it we can categorise points into two types:
Collinear points;
Non-collinear points.
Collinear and Non-collinear points
We say 3 or more points are collinear if they all lie on a straight line.
Otherwise, they are non-collinear.
Collinear points, StudySmarter Original
In the diagram above points A, B, C, and D all lie in the same line and so they are collinear points.
Non-collinear points, StudySmarter Original
Now, in the diagram above there is no line that could be drawn connecting all the four points A, B, C, and D. Therefore, they are non-collinear points.
Now, non-collinear points open up the world of Geometry even more.
Given three non-collinear points we can draw exactly one plane which contains all of the three points. Also given a line and a point, only one plane can contain both of them. Similarly, given two parallel lines only one plane can contain all of them.
Three points, two lines, or a line and a point exterior to the line form a plane, StudySmarter Original
Now suppose we have 4 or more points, then we ask the question, do they exist in the same plane. Depending on it, we can categorise a set of points into
Coplanar points
Non-coplanar points
Coplanar and Non-coplanar points
If a set of points lie on the same plane, they are called coplanar points.
Otherwise they non-coplanar points.
Coplanar points, StudySmarter Original
If two or more lines meet at a point, it is called the point of concurrency.
Point of concurrency, StudySmarter Original
Identify the points, collinear points, non-collinear and concurrent points from the below figure.
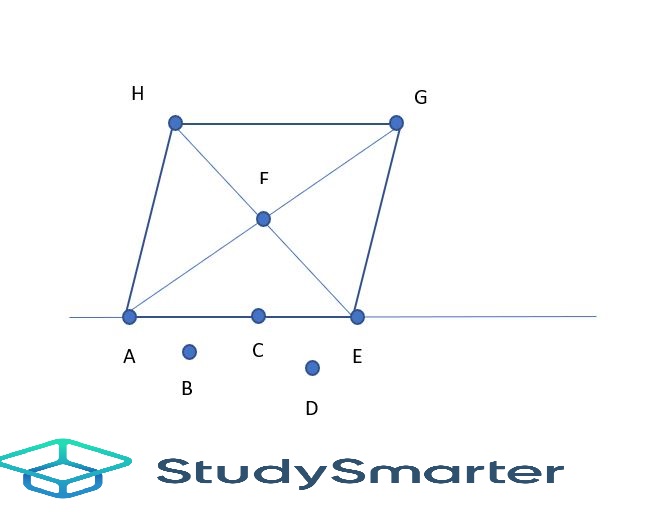
Solution
The points are A, B, C, D, E, F, G and H.
The set of collinear points are {A, C, E}, {A, F, G}, and {H, F, E}. The points B and D are not collinear with another two points.
Point F is a concurrent point of the lines .
In the diagram below we have some points in 3 dimensions.
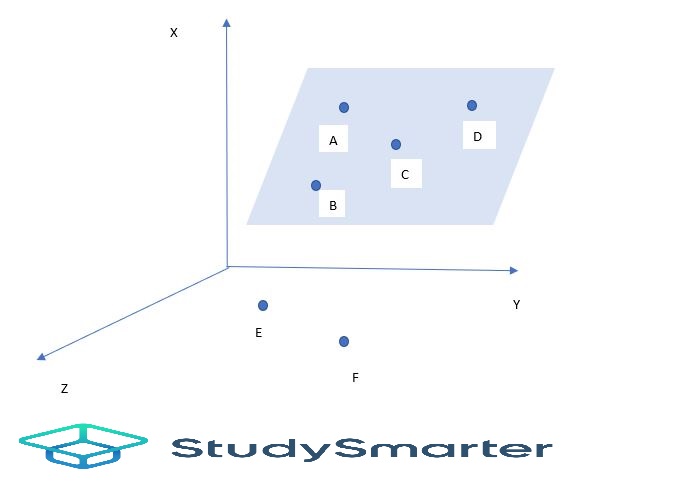
The points that lie in the same plane are A, B, C, and D. The points E and F are outside this plane.
Types of lines
As we saw before, a line extends in both directions. Lines can be straight and curved. When lines are straight, we can categorise lines as one of the three below.
Horizontal line
Vertical line
Oblique line
Types of lines, StudySmarter Original
Observing the picture above, we can say that,
Real-life examples
- Horizontal lines - The edges of the steps on the staircase.
- Vertical lines - A row of tall trees on highways.
- Oblique line - The Handel of the staircase.
When we have two lines then they either intersect or do not intersect at any point. Depending on this we have
Parallel lines
Intersecting lines
Parallel and intersecting lines
We say two lines are parallel if they do not have any point of intersection.
If two lines intersect, then they are intersecting lines.
When two lines intersect they intersect at a point. In particular, if the angle between the two lines is 90º, then they are called perpendicular lines.
Parallel, intersecting and perpendicular lines, StudySmarter OriginalTypes of planes
Similar to that of two lines we can categorise given two planes as either
Parallel planes or
Intersecting planes
When two planes never intersect each other they are called parallel planes.
Otherwise, they are called intersecting planes.
When two planes intersect they intersect along a line. And, similarly to lines, planes can also intersect at an angle of 90º, which are called perpendicular planes.
Parallel and intersecting planes, StudySmarter Original
Points, Lines, and Planes - Key takeaways
- The point is dimensionless, line is one-dimensional and plane is two-dimensional object.
- Numerous straight lines can be drawn with one point. Only one line can be drawn through two given points. If three or more points lie in the same line we call them collinear. Otherwise they are non-collinear points.
- There is exactly one plane which contains 3 non-collinear points, a line and a point, and 2 parallel lines. When two or more points or two or more lines lie in the same plane they are called co-planar. Otherwise, they are non-coplanar.
- Two lines intersect at a point. A line intersects a plane at one point. The meeting point of the two planes is a straight line.
Explanations 
Exams 
Magazine 
