
Road sign and coloured paper example, StudySmarter Originals
Do you see any resemblances between this road sign and each sheet of paper? As a matter of fact, there are two similarities we can spot here! First of all, both objects have exactly four sides. Secondly, they have precisely four corners on each side. You may now be wondering, what kind of shape might have such properties and if so, what are they called? To answer your question, these shapes are called quadrilaterals!
In this discussion, we shall be introduced to a particular type of polygon known as a quadrilateral. Here, we shall look at the different types of quadrilaterals while studying their properties, perimeter and area formulas.
What is a Quadrilateral?
The abbreviation "quad" describes something that is in terms of four. For example, a mother carrying four babies in one pregnancy will be expecting the birth of quadruplets. In geometry, this contraction is found in the term quadrilateral, which adopts the same idea. Let's define it below.
A quadrilateral is a polygon with four sides, four vertices and four angles.
Recall that a polygon is a two-dimensional geometric figure with a finite number of sides.
The sides (or edges) of a polygon are made up of straight-line segments joined together end to end. The point at which a pair of line segments meet is called the vertex (or corner).
The term quadrilateral stems from two Latin words: quadri (a variant of four) and latus (side). There are two other names that describe a quadrilateral, namely
- A tetragon which is derived from the Greek words tetra and gon meaning four and angle (or corner), respectively;
- A quadrangle since it has four angles.
Naming a Quadrilateral
It is important to note that the order of the vertices for a given quadrilateral must be taken into account when naming a quadrilateral. Here is an example.
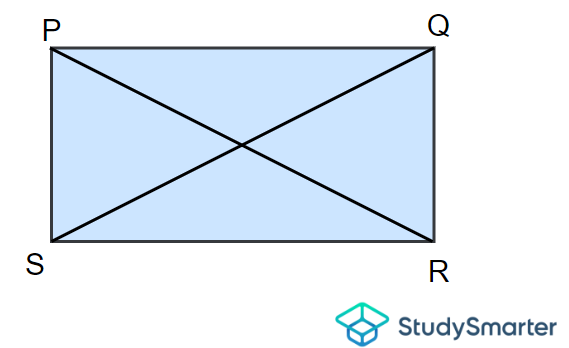
Naming a quadrilateral, StudySmarter Originals
The quadrilateral above has sides \(PQ\), \(QR\), \(RS\) and \(SP\) and vertices \(P\), \(Q\), \(R\) and \(S\). The diagonals are described by \(PR\) and \(QS\).
This quadrilateral can be denoted by \(PQRS\), \(QRSP\), \(RSPQ\) or \(SPQR\). However, we cannot call it \(SQPR\) or \(RPQS\), for example since the order of the vertices here is incorrect.
Types of Quadrilaterals
There are six types of quadrilaterals we should familiarise ourselves with throughout this topic. This is described in the table below.
Quadrilateral | Visual Representation |
Square | 
Square, StudySmarter Originals |
Rectangle | 
Rectangle, StudySmarter Originals |
Parallelogram | 
Parallelogram, StudySmarter Originals |
Trapezium | 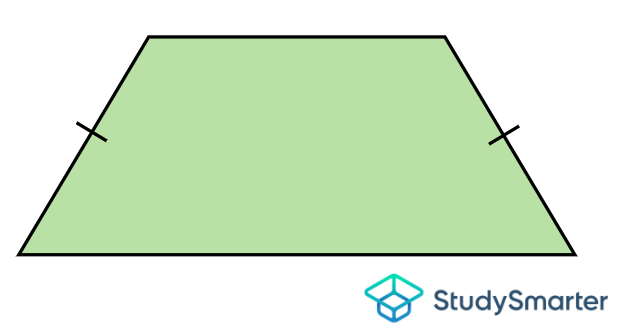
Trapezium, StudySmarter Originals |
Rhombus | 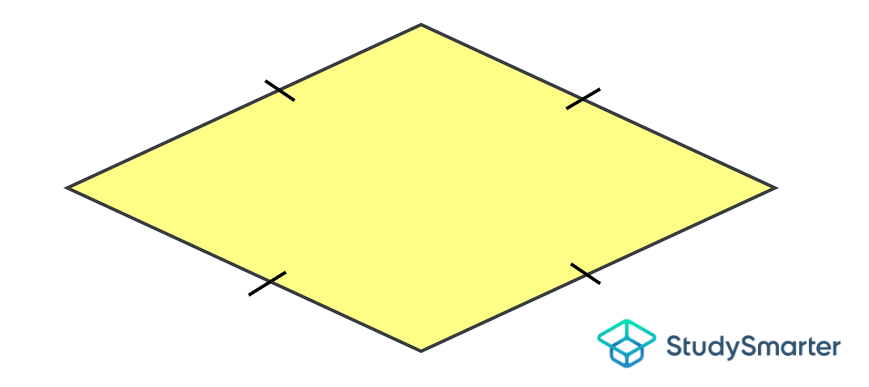
Rhombus, StudySmarter Originals |
Kite | 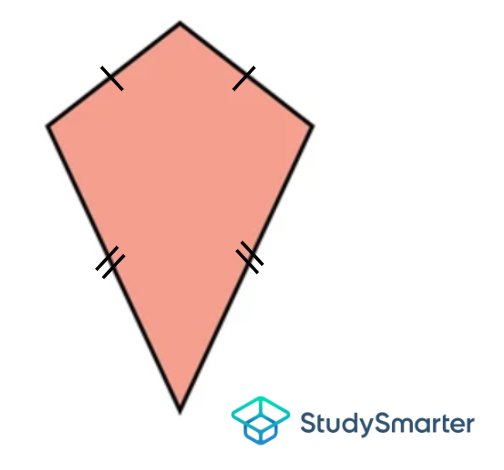
Kite, StudySmarter Originals |
Properties of Quadrilaterals
Looking at our previous table, there are four characteristics all quadrilaterals have in common. Listing them below, we can say that every quadrilateral has
Four sides;
Four vertices;
Two diagonals;
The sum of all their interior angles is 360o.
Although all quadrilaterals have the same basic qualities, the measures of their sides and angles differ from one another. In the table below, we shall describe the distinct features of the six quadrilaterals introduced before.
Quadrilateral | Sides | Parallel Sides | Angles | Right Angles | Diagonals |
Square 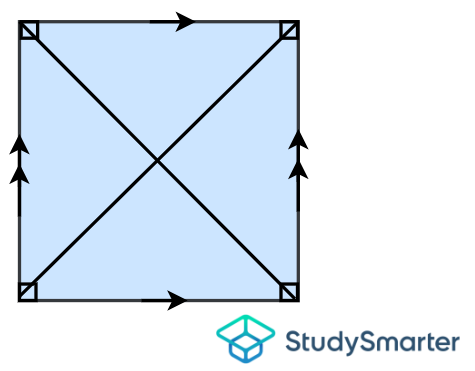
Square, StudySmarter Originals | Has 4 equal sides | Has 2 pairs of parallel sides | Has 4 equal angles | Has 4 right angles | Has 2 equal diagonals that are perpendicular and bisect each other |
Rectangle 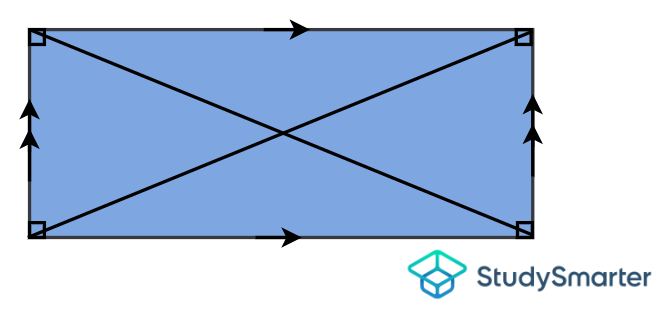
Rectangle, StudySmarter Originals | Has opposite sides of equal length | Has 2 pairs of parallel sides | Has 4 equal angles | Has 4 right angles | Has 2 equal diagonals that bisect each other |
Parallelogram 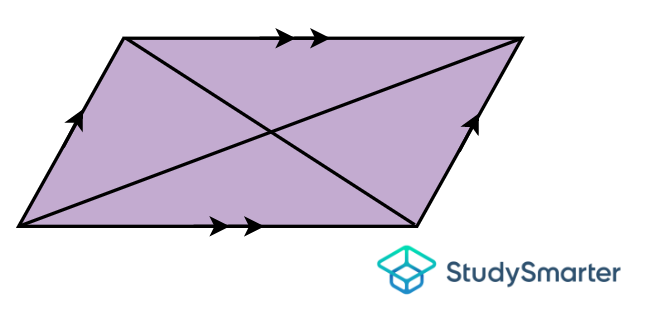
Parallelogram, StudySmarter Originals | Has opposite sides of equal length | Has 2 pairs of parallel sides | Has opposite angles of equal measures | None | Has 2 non-equal diagonals that bisect each other |
Trapezium 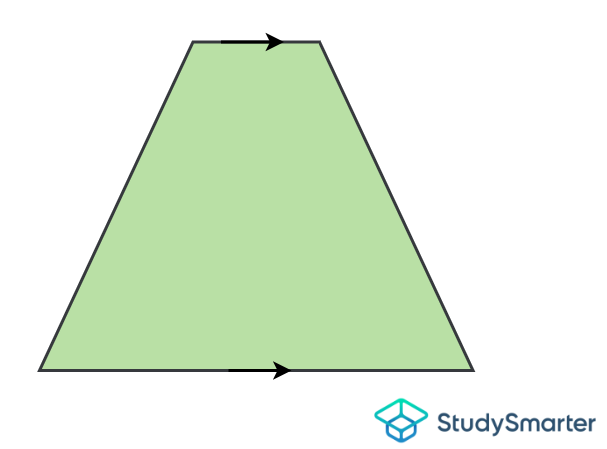
Trapezium, StudySmarter Originals | Legs: The sides that are not parallel to each other If there are two equal legs, it is called an isosceles trapezium
| | If there are no angles (or sides) of equal measure, it is called a scalene trapezoid. If there are two opposite obtuse angles, it is called an obtuse trapezoid. If there are two adjacent acute angles, it is called an acute trapezoid.
| If there are two adjacent right angles, it is called a right trapezium. 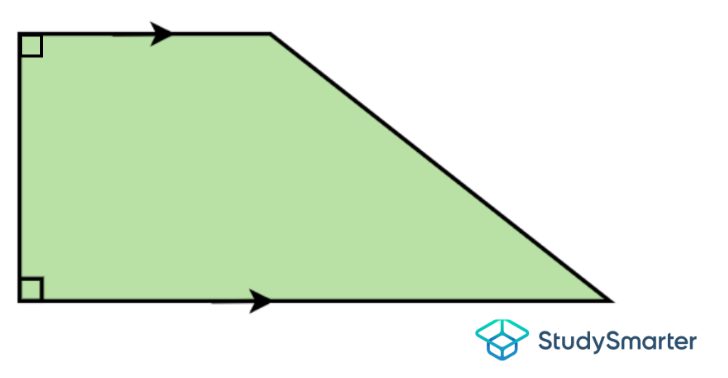
Right trapezium, StudySmarter Originals | If the diagonals are of equal lengths, it is an isosceles trapezoid. 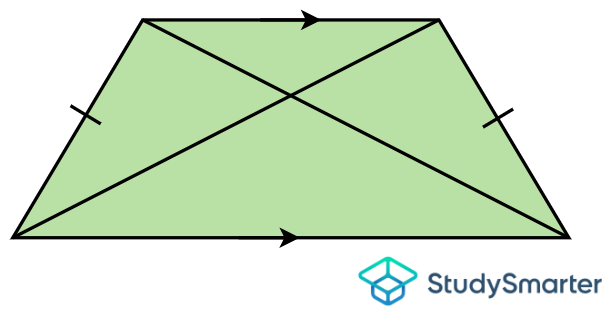
Isosceles trapezium, StudySmarter Originals |
Rhombus 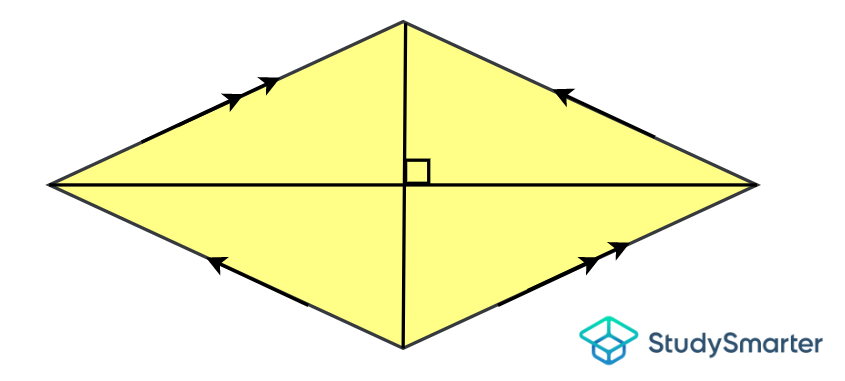
Rhombus, StudySmarter Originals | Has 4 equal sides | Has 2 pairs of parallel sides | Has opposite angles of equal measures | None | Has 2 non-equal diagonals that are perpendicular and bisect each other |
Kite 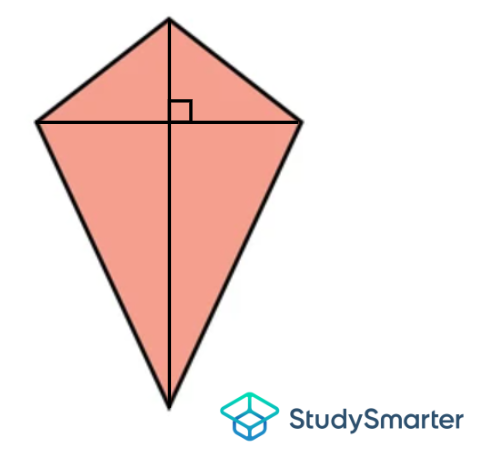
Kite, StudySmarter Originals | Has two pairs of equal adjacent sides | None | Has one pair of equal opposite angles that are obtuse | None | Has 2 non-equal diagonals that are perpendicular and bisect each other |
Angles of Quadrilaterals
In this segment, we shall discuss the characteristics of the interior and exterior angles of a quadrilateral. We shall also observe some notable relationships between their opposite and adjacent angles.
Interior Angles of a Quadrilateral
We had mentioned before that the sum of the interior angles of a quadrilateral is \(360º\). Since a quadrilateral is a type of polygon, we can prove this statement by using the following formula.
Sum of Interior Angles Formula
For a polygon with n number of sides, the sum of its interior angles, S is equal to
\[S=(n-2)\times 180º\]
Since a quadrilateral has four sides, then \(n = 4\) and so
\[S=(4-2)\times 180º\]
\[\implies S=2\times 180º\]
\[\implies S=360º\]
Thus, we have shown that all the interior angles of a quadrilateral add up to \(360º\).

Interior angles of a quadrilateral, StudySmarter Originals
In the rectangle above, \(\angle SPQ + \angle PQR + \angle QRS + \angle RSP = 360º\).
Adjacent Angles of Quadrilaterals
Two angles that lie side by side are called adjacent angles. Adjacent angles often make use of two important concepts, namely
Supplementary angles: Two adjacent angles are supplementary when the sum of their measures is equal to \(180º\).
Complementary angles: Two adjacent angles are complementary when the sum of their measures is equal to \(90º\).
Both these ideas can be applied to quadrilaterals as well. Let us observe the rhombus below.
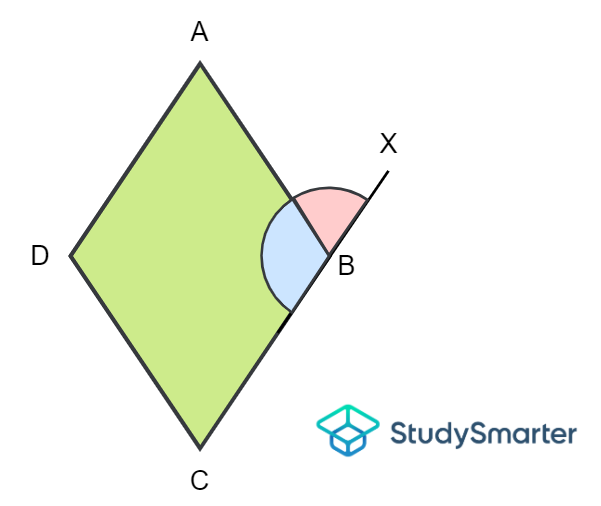
Supplementary angles of a quadrilateral, StudySmarter Originals
The straight line segment \(CBX\) is made up of \(\angle ABC\) (interior angle of the rhombus) and \(\angle ABX\) (exterior angle of the rhombus). The angle of a straight line is always \(180º\). Since \(\angle ABC\) and \(\angle ABX\) lie on this line and are adjacent to each other, they are supplementary angles. Say we are given \(\angle CBA = 114º\). To find \(\angle ABX\), we can conduct the following calculation.
\[\angle ABC + \angle ABX=\overline{CBX}\]
\[\implies \angle ABC+114º=180º\]
\[\implies \angle ABC=180º-114º\]
\[\implies \angle ABC=66º\]
Thus, \(\angle ABX=66º\). Now, let us take a look at the rectangle below.

Complementary angles of a quadrilateral, StudySmarter Originals
Given the properties of a rectangle, we know that each interior angle is \(90º\). Say \(\angle RSQ = 22º\). We are now told to find \(\angle PSQ\). To do this, simply note that the sum of \(\angle RSQ\) and \(\angle PSQ\) equal \(90º\) since they are adjacent and lie at a right angle. Thus, \(\angle PSQ\) is \(68º\) since
\[\angle PSQ + \angle RSQ=\angle PSR\]
\[\implies \angle PSQ+22º=180º\]
\[\implies \angle PSQ=180º-22º\]
\[\implies \angle PSQ=68º\]
Exterior Angles of a Quadrilateral
The sum of the exterior angles of any polygon equals \(360º\). This means that the sum of the exterior angles of a quadrilateral is also \(360º\). To show this, let us return to our previous rectangle and draw an extended straight line at each vertex.
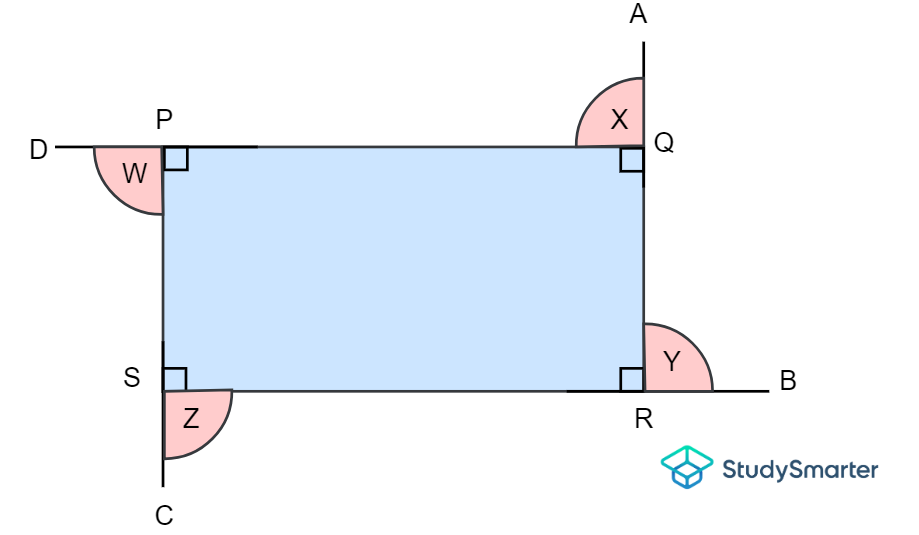
Exterior angles of a quadrilateral, StudySmarter Originals
The interior angles of this rectangle are \(\angle SPQ\), \(angle PQR\), \(\angle QRS\) and \(\angle RSP\), while the exterior angles are \(\angle W\), \(\angle X\), \(\angle Y\) and \(\angle Z\). Notice that each interior angle corresponds to an exterior angle that is adjacent to them and lies on a straight line. Recall that the angle of a straight line is \(180º\). Thus, we have four sets of supplementary angles. The exterior angles in this case are also equal since the interior angles are all equal. Let's solve one of these exterior angles to prove our claim.
\[\angle PQR=\angle X=\overline{RQA}\]
\[\implies \angle PQR+90º=180º\]
\[\implies \angle PQR=180º-90º\]
\[\implies \angle PQR=90º\]
Since, \(\angle X = \angle Y = \angle Z = \angle W= 90º\), then \(\angle X + \angle Y + \angle Z + \angle W = 9(90º)= 360º\), as required.
Vertically Opposite Angles of Quadrilaterals
Vertically opposite angles are two (opposite) angles constructed by two straight intersecting lines that extend from a pair of distinct vertices. Vertically opposite angles are always equal to each other. Refer back to our rectangle above with O being the point of intersection between the two diagonals.
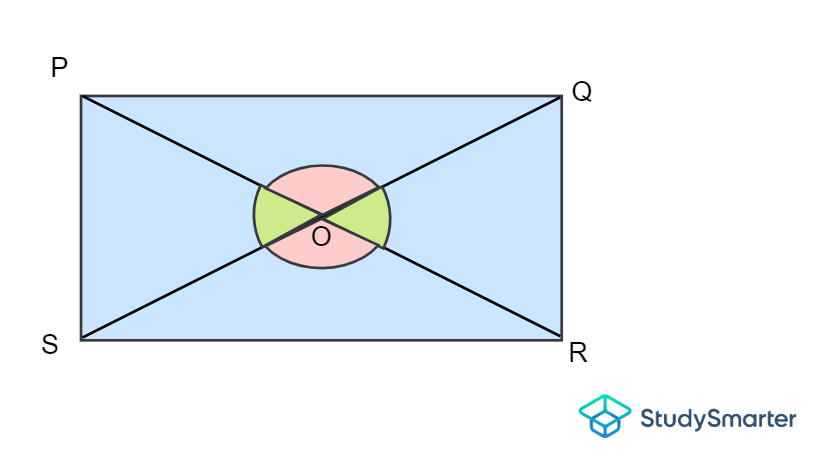
Vertically opposite angles of a quadrilateral, StudySmarter Originals
Here, \(\angle POQ\) and \(\angle SOR\) are vertically opposite angles. Thus, \(\angle POQ = \angle SOR\). Similarly, \(\angle POS\) and \(\angle QOR\) are vertically opposite angles and so \(\angle POS =\angle QOR\). The same concept applies to squares, rectangles, parallelograms, rhombuses and kites (try it yourself!).
Corresponding Angles of Quadrilaterals
Corresponding angles are formed when two parallel lines are intersected by the transversal line. A transversal line is a line that crosses a pair of lines on the same plane at two specific points. Corresponding angles are always equal to each other. Let's show this with the parallelogram below.
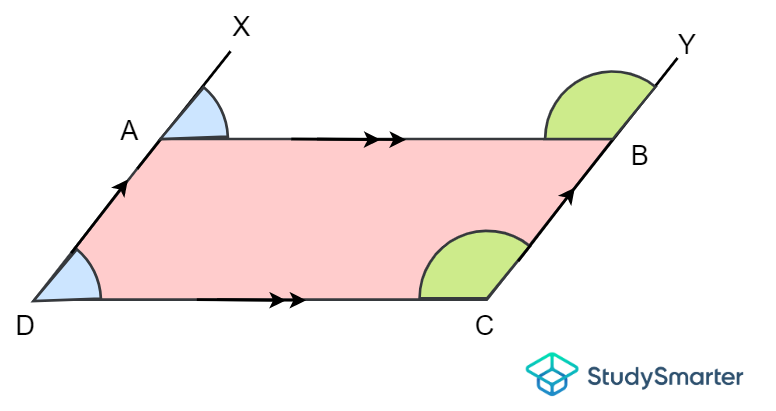
Corresponding angles of a quadrilateral, StudySmarter Originals
Here, \(\angle ADC\) (interior angle of the parallelogram) and \(\angle XAB\) (exterior angle of the parallelogram) are corresponding angles since the line \(DAX\) passes through parallel sides \(AB\) and \(DC\). Thus, \(\angle ADC = \angle XAB\).
Similarly, \(\angle BCD\) and \(\angle YBA\) are corresponding angles since the line \(CBY\) crosses the parallel sides \(AD\) and \(BC\). Therefore, \(\angle BCD = \angle YBA\). This concept applies to squares, rectangles and rhombuses as well (give it a go!).
Perimeter of Quadrilaterals
The perimeter of a quadrilateral is defined as the total length of its boundary. In other words, it is the sum of all its sides. Therefore, for a quadrilateral \(ABCD\)
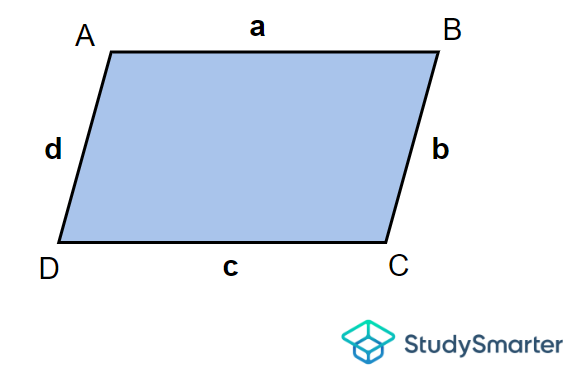
The perimeter of quadrilaterals, StudySmarter Originals
with sides \(AB\), \(BC\), \(CD\) and \(DA\), the perimeter, \(P\) is
\[P=\overline{AB}+\overline{BC}+\overline{CD}+\overline{DA}\]
or
\[P=a+b+c+d\]
Here are two examples.
Find the perimeter of the parallelogram below.
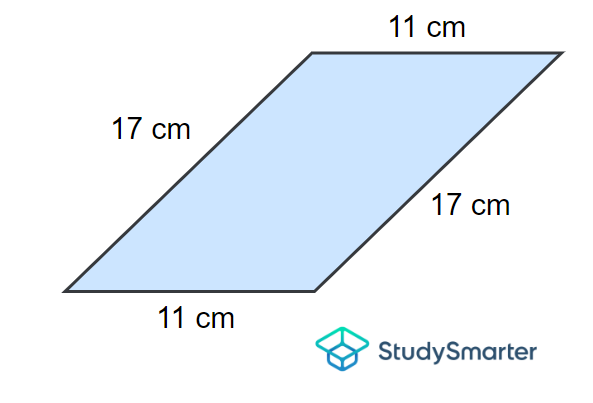
Example 1, StudySmarter Originals
Solution
To solve this, we shall simply add the dimensions of all four sides of this parallelogram.
\[P=17+17+11+11\]
\[\implies P=2(17)+2(11)\]
\[\implies P=34+22\]
\[\implies P=56\,\mathrm{cm}\]
Thus, its perimeter is \(56 \,\mathrm{cm}\).
Calculate the length of the missing side, \(x\) of the trapezoid below given that the perimeter is \(51\,\mathrm{cm}\).
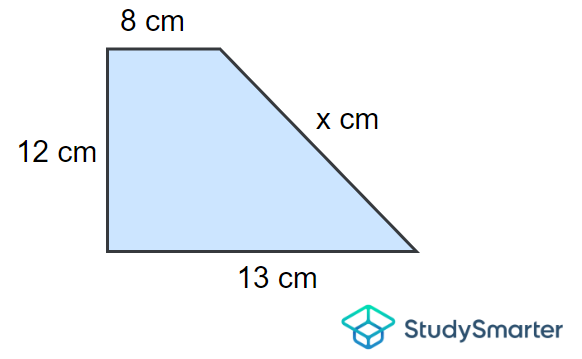
Example 2, StudySmarter Originals
Solution
Using the formula for the perimeter of a quadrilateral, we find that
\[P=8+12+13+x\]
\[\implies 51=8+12+13+x\]
\[\implies 8+12+13+x=51\]
Now bringing \(8\), \(12\) and \(13\) to the right-hand side of this equation, thus making \(x\) the subject, we obtain
\[x=51-8-12-13\]
\[\implies x=18\,\mathrm{cm}\]
Therefore, the length of the missing side, \(x\) is \(18\, \mathrm{cm}\).
Area of Quadrilaterals
The area of a quadrilateral is described by the space enclosed within its boundary. Each of the six types of quadrilaterals we have seen above has its own area formula. The table below presents their respective area formulas.
Quadrilateral | Area |
Square 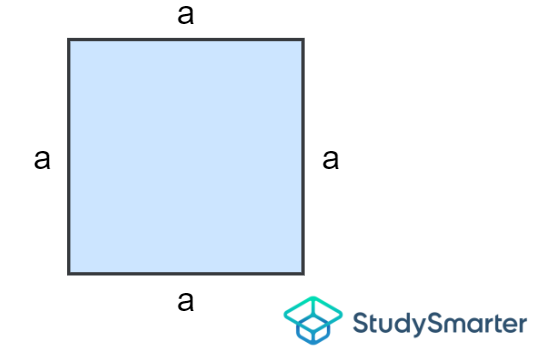
Area of a square, StudySmarter Originals | \[A=a\times a=a^2\] where \(a\) is the length of each side. |
Rectangle 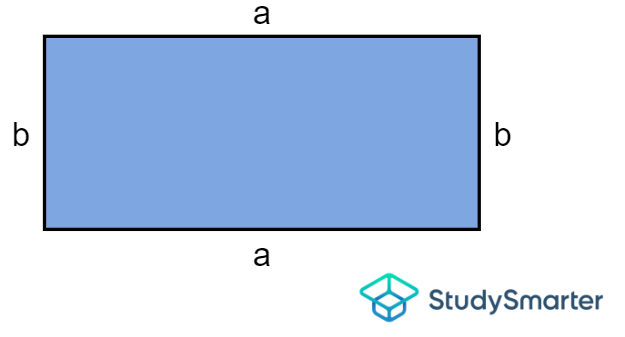
Area of a rectangle, StudySmarter Originals | \[A=a\times b\] where \(a\) and \(b\) are the lengths of width and height, respectively. |
Parallelogram 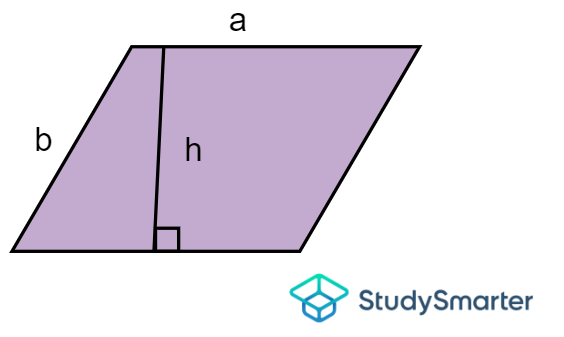
Area of a parallelogram, StudySmarter Originals | \[A=a\times h\] where \(a\) and \(h\) are the lengths of width and height, respectively. |
Trapezium 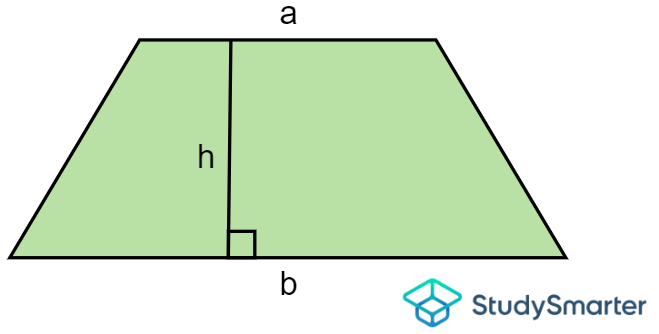
Area of a trapezium, StudySmarter Originals | \[A=\dfrac{1}{2}\times (a+b)\times h\] where \(a\) and \(b\) are the lengths of the bases (top and bottom parallel sides) and h is the height. |
Rhombus 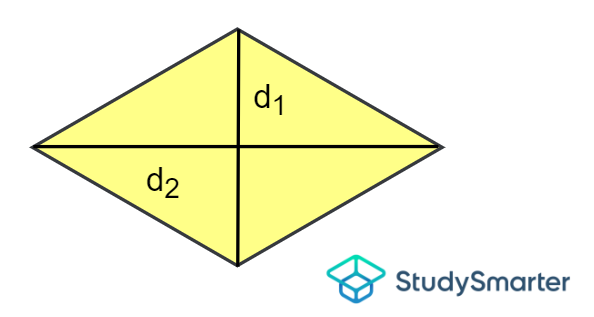
Area of a rhombus, StudySmarter Originals | \[A=\dfrac{1}{2}\times d_1\times d_2\] where \(d_1\) and \(d_2\) are the lengths of the vertical diagonal and horizontal diagonal, respectively. |
Kite 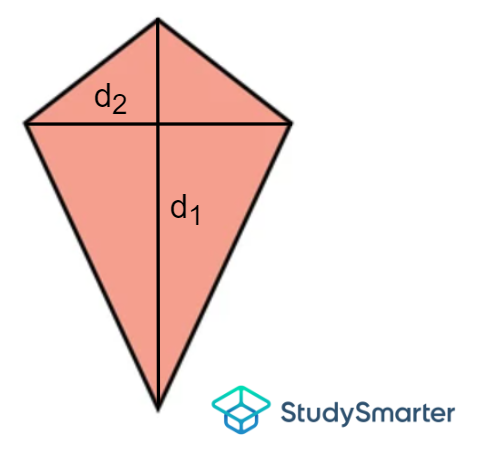
Area of a kite, StudySmarter Originals | \[A=\dfrac{1}{2}\times d_1\times d_2\] where d1 and d2 are the lengths of the vertical diagonal and horizontal diagonal, respectively. |
Let us look at two worked examples.
Find the area of the trapezium below.
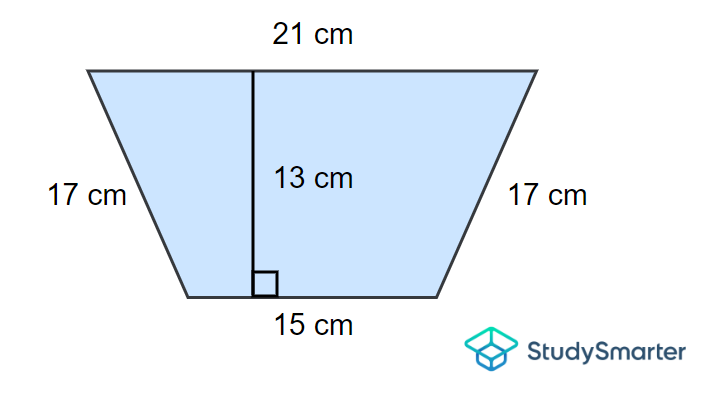
Example 3, StudySmarter Originals
Solution
From the diagram above we can deduce that
\[a = 21\, \mathrm{cm}\]
\[b = 15\, \mathrm{cm}\]
\[h = 13\, \mathrm{cm}\]
Now using the area formula for a trapezium, we obtain
\[A=\dfrac{1}{2}\times (21+15)\times 13\]
\[\implies A=\dfrac{1}{2}\times (36)13\]
\[\implies A=\dfrac{1}{2}\times 468\]
\[\implies A=234\,\mathrm{cm}^2\]
Important note: Don't be confused by the length of the bases and legs! The parallel sides are the bases which are what we will use in our formula.
Thus the area is \(234\, \mathrm{cm}^2\).
Find the length of the horizontal diagonal, d of the rhombus below given that the area is \(123.5\, \mathrm{cm}\).
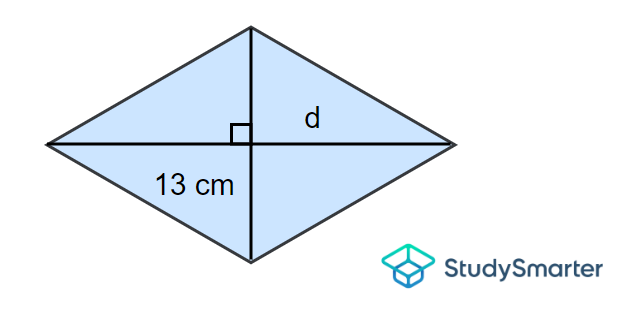
Example 4, StudySmarter Originals
Solution
Here, the vertical diagonal is \(13\,\mathrm{cm}\). Using the area formula of a rhombus, we find that
\[A=\dfrac{1}{2}\times 13\times d\]
\[\implies 123.5=\dfrac{1}{2}\times 13\times d\]
\[\implies \dfrac{13\times d}{2}=123.5\]
Now multiplying both sides by \(2\), we obtain
\[\cancel{2}\left(\dfrac{13\times d}{\cancel{2}}\right)=2(123.5)\]
\[\implies 13d=247\]
Then dividing both sides by \(13\), we get
\[\dfrac{\cancel{13}d}{\cancel{13}}=\dfrac{247}{13}\]
\[\implies d=19\,\mathrm{cm}\]
Thus, the length of the horizontal diagonal, \(d\) is \(19\, \mathrm{cm}\).
Examples Involving Quadrilaterals
We shall end this topic with several worked examples of quadrilaterals that make use of the concepts we have established throughout this discussion.
Given the kite \(ABCD\) below, answer the following questions:
Find the missing sides \(AD\) and \(AB\), given that the perimeter is \(88\,\mathrm{cm}\).
Calculate the missing angles \(M\) and \(N\).
Are any of these sides parallel to each other?
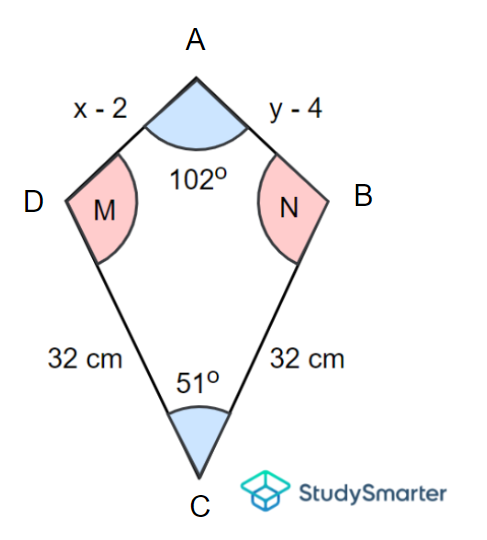
Example 5, StudySmarter Originals
Question 1
Firstly, note that \(AD = AB\) since a kite has two pairs of equal adjacent sides (the other being \(CB = CD\)).
\[AD=AB\]
\[\implies x-2=y-4\]
\[\implies y=x-2+4\]
\[\implies y=x+2\]
Now, given the perimeter and the sum of all its sides, we obtain
\[P=AB+AD+CD+CD\]
\[\implies 88=(y-4)+(x-2)+32+32\]
\[\implies 88=y+x-6+64\]
Now substituting for \(y\) and solving this equation for \(x\), we obtain
\[88=(x+2)+x-6+64\]
\[\implies (x+2)+x-6+64=88\]
\[\implies 2x+60=88\]
\[\implies 2x=88-60\]
\[\implies 2x=28\]
Now dividing both sides by \(2\), have
\[x=\dfrac{28}{2}\]
\[\implies x=14\]
Thus, the lengths of \(AB\) and \(AD\) are
\[AB=y-4\]
\[\implies AB=(x+2)-4\]
\[\implies AB=(14+2)-4\]
\[\implies AB=12\,\mathrm{cm}\]
Since \(AB = AD\), thus \(AD\) is also \(12\, \mathrm{cm}\).
Question 2
Recall that a kite has one pair of equal opposite angles that are obtuse. This means that \(M = N\). Furthermore, that measures of the other two angles are given and the sum of all the interior angles of any quadrilateral is \(360º\). From here, we find that
\[\angle DAB+\angle BCD+\angle M+\angle N=360º\]
\[\implies 102º+51+\angle M+\angle N=360º\]
\implies 153º+2\angle M=360º\]
Now solving for \(M\), we obtain
\[2\angle M=360º-153º\]
\[\implies 2\angle M=207º\]
\[\implies \angle M=\dfrac{207º}{2}\]
\[\implies \angle M=103,5º\]
Thus, both \(M\) and \(N\) are equal to \(103.5º\) (since \(M = N\)).
Question 3
By the properties of a kite, there are no sides that are parallel to each other.
Given the parallelogram \(ABCD\) below, answer the following questions:
Find the length of \(AB\) given that the perimeter is \(40\, \mathrm{cm}\).
Calculate the area of \(ABCD\).
Deduce the angle \(Y\).
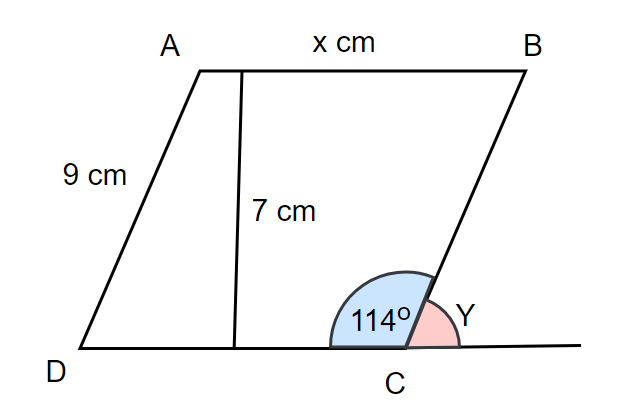
Example 6, StudySmarter Originals
Question 1
Firstly, note that \(AB = DC\) and \(AD = BC\) since a parallelogram has two pairs of equal opposite sides. Given the perimeter and the sum of all its sides, we obtain
\[P=AB+AD+CD+CD\]
\[\implies 40=x+9+x+9\]
\[\implies 40=2x+18\]
Now solving this equation for \(x\), we obtain
\[2x=40-18\]
\[\implies 2x=22\]
\[\implies x=\dfrac{22}{2}\]
\[\implies x=11\,\mathrm{cm}\]
Thus, the length of \(AB\) is \(11\, \mathrm{cm}\).
Question 2
Here, the height is \(7\, \mathrm{cm}\) and the width is the length of side \(AB\). We know that \(AB\) is equal to \(11\, \mathrm{cm}\). Thus, by the area formula of a parallelogram, we have
\[A=11\times 7\]
\[\implies 77\,\mathrm{cm}^2\]
Thus, the area of \(ABCD\) is \(77\,\mathrm{cm}^2\).
Question 3
In this case, \(\angle BCD\) and \(\angle Y\) are supplementary since both these angles are on a straight line. Recall that two angles are supplementary when the sum of their measures is equal to \(180º\). Using this idea, we find that
\[\angle BCD+\angle Y=180º\]
\[\implies 114º+\angle Y=180º\]
Now, rearranging this equation and solving for our missing angle, we obtain
\[\angle Y=180º-114º\]
\[\implies \angle Y=66º\]
Thus \(Y\) is equal to \(66º\).
Given the rectangle \(PQRS\) below, answer the following questions:
Find the perimeter and area of \(PQRS\).
Calculate the length of the diagonal \(QS\).
How big is \(\angle QSR\)?
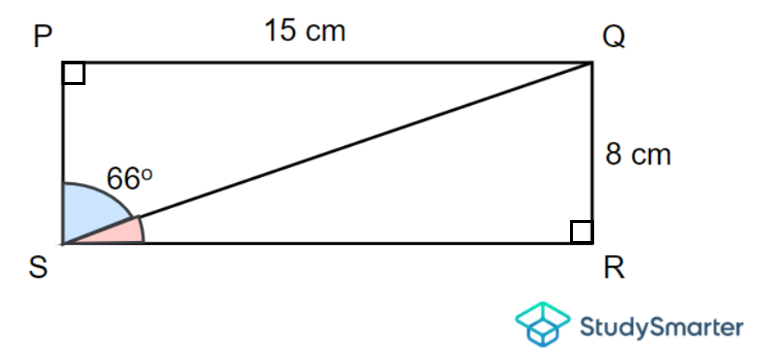
Example 7, StudySmarter Originals
Question 1
Firstly, note that \(PQ = SR\) and \(PS = QR\) since a rectangle has two pairs of equal opposite sides. Now, adding the lengths of all its sides, we obtain
\[P=PQ+QR+SR+PS\]
\[\implies P=15+8+15+8\]
\[\implies P=46\,\mathrm{cm}\]
Here, the length is \(15\,\mathrm{cm}\) and the height is \(8\, \mathrm{cm}\). So by the area formula of a rectangle, we find that
\[A=15\times 8\]
\[\implies A=120\,\mathrm{cm}^2\]
Thus, the perimeter is \(46\, \mathrm{cm}\) and the area is \(120\,\mathrm{cm}^2\).
Question 2
By the properties of a rectangle, recall that it has 4 right angles. Notice that the diagonal \(QS\) creates a right-angle triangle \(QRS\) where \(\angle QRS\) is equal to \(90º\). Thus, we can use Pythagoras' Theorem to find the length of \(QS\). Here, \(QS\) is the hypotenuse and the two sides are \(QR = 8 \,\mathrm{cm}\) and \(SR = 15\, \mathrm{cm}\). By doing so, we get
\[QS^2=QR^2+SR^2\]
\[\implies QS^2=8^2+15^2\]
\[\implies QS^2=64+225\]
\[\implies QS^2=289\]
We will only consider the positive root since we are dealing with measurements. Then
\[QS=\sqrt{289}\]
\[\implies QS=17\,\mathrm{cm}\]
Thus, the diagonal, \(QS\) is equal to \(17\,\mathrm{cm}\).
Question 3
Here, \(\angle PSQ\) and \(\angle QSR\) are complementary since both these angles lie at a right angle. Recall that two angles are complementary when the sum of their measures is equal to \(90º\). With that, we have
\[\angle PSQ+\angle QSR=90º\]
\[\implies 66º+\angle QSR=90º\]
Now, rearranging this equation and solving for our missing angle, we obtain
\[\angle QSR=90º-66º\]
\[\implies \angle QSR=24º\]
Thus \(\angle QSR\) is equal to \(24º\).
Quadrilaterals - Key takeaways
- A quadrilateral is a polygon with four sides, four vertices and four angles.
- A quadrilateral has two diagonals.
- The sum of all the interior angles of a quadrilateral is \(360º\).
- There are six types of quadrilaterals: square, rectangle, parallelogram, trapezium, rhombus and kite.
- The perimeter of a quadrilateral is the sum of all its sides, i.e. \(P = a + b + c + d\)
- Area formula for quadrilaterals
Quadrilateral | Area |
Square | \(A=a\times a=a^2\) |
Rectangle | \(A=a\times b\) |
Parallelogram | \(A=a\times h\) |
Trapezium | \(A=\dfrac{1}{2}\times (a+b)\times h\) |
Rhombus | \(A=\dfrac{1}{2}\times d_1\times d_2\) |
Kite | \(A=\dfrac{1}{2}\times d_1\times d_2\) |









































