Sum and Difference of Angles Formulas

In a class of trigonometry, our Maths teacher said that the sum of 30° and 40° would give 70° but the sum of sin30° and sin40° would not give sin70° and that caused some commotion in the class. How then do you add and subtract sines or cosines of angles? Hereafter, all you need to know about such operations will be explained.

What are the sum and difference of angles formulas in trigonometry?

Unlike normal arithmetic operations, addition and subtraction of trigonometric functions have a different approach. For example, cos (45° -15°) is not the same as cos45° - cos15°. It becomes more challenging when trigonometric functions are involved in such arithmetic operations. So, formulas have to be derived to carry out to solve this problem.

Having the knowledge of the trigonometric functions of special angles such as sines, cosines, and tangents of 30, 45, 60, and 90 degrees, means that the addition or subtraction of these angles can give other angles. For instance, sin15° can be derived, since sin15° is the same as sin(45-30)° . Afterwards, we shall be deriving formulas to solve these operations.

Proving Sum and Difference of Cosine Functions

Difference of cosine functions

Consider the figure below:

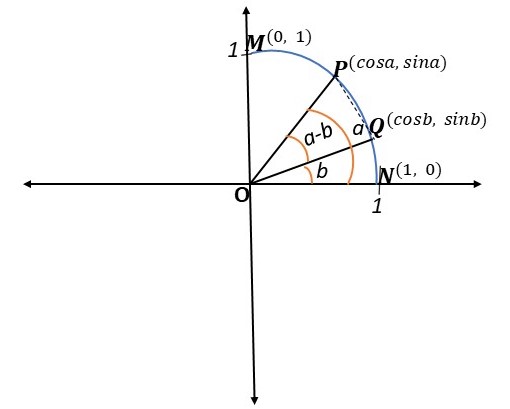
Figure 1: An image showing the use of the standard position of a unit circle to prove the difference of cosine functions, - StudySmarter Originals

$d=\sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2}$

Where in point P, $(x_2,y_2)$ is$(\cos a,\sin a)$ and in point Q, $(x_1,y_1)$ is$(\cos b,\sin b)$. Thus

$$\begin{gathered} PQ=\sqrt{(cosa-cosb{)}^2+(sina-sinb{)}^2} \\ P{Q}^2=(cosa-cosb{)}^2+(sina-sinb{)}^2 \\ P{Q}^2=co{s}^{2}a-2cosacosb+co{s}^{2}b+si{n}^{2}a-2sinasinb+si{n}^{2}b \end{gathered}$$

Rearrange the equation

$P{Q}^2=co{s}^{2}a+si{n}^{2}a+co{s}^{2}b+si{n}^{2}b-2cosacosb-2sinasinb$

Remember:

$co{s}^2\theta +si{n}^2\theta =1;so,co{s}^{2}a+{\sin }^{2}a=1andsi{n}^{2}b+{\cos }^{2}b=1$

$$\begin{gathered} P{Q}^2=1+1-2cosacosb-2sinasinb \\ P{Q}^2=2-2cosacosb-2sinasinb \end{gathered}$$

If the angle (a-b) were to be replotted into the standard position of a unit circle from the origin O to the point S in the figure below

Figure 2: An image of the angle (a-b) being replotted, - StudySmarter Originals

Using

$d=\sqrt{{(x_2-x_1)}^2+{(y_2-y_1)}^2}$

Where point S is $(x_2,y_2)$ and N is $(x_1,y_1)$, then

$$\begin{gathered} SN=\sqrt{(\cos {(a-b)-1)}^2+(\sin {(a-b)-0)}^2} \\ S{N}^2=(\cos {(a-b)-1)}^2+(\sin {(a-b)-0)}^2 \\ S{N}^2={\cos }^2(a-b)-2\cos (a-b)+1+{\sin }^2(a-b) \end{gathered}$$

Rearrange and bring like terms

$S{N}^2={\cos }^2(a-b)+{\sin }^2(a-b)-2\cos (a-b)+1$

Remember that

$co{s}^2\theta +si{n}^2\theta =1;so,co{s}^2(a-b)+{\sin }^2(a-b)=1$

then;

$$\begin{gathered} S{N}^2=1-2\cos (a-b)+1 \\ S{N}^2=2-2\cos (a-b) \end{gathered}$$

Remember that

$PQ=SN$

then

$P{Q}^2=S{N}^2$

Thus

$2-2\cos (a-b)=2-2\cos a\cos b-2\sin a\sin b$

Solve the algebra by subtracting 2 from both sides of the equation

$-2\cos (a-b)=-2\cos a\cos b-2\sin a\sin b$

Divide both sides by -2 on both sides

$\cos (a-b)=\cos a\cos b+\sin a\sin b$

Summing of cosine functions

$cos(a+b)=\cos (a-(-b\left)\right)$

Thus, substitute the value of b as -b in the equation.

Note that

$\cos (-b)=\cos b$

and

$\sin (-b)=-\sin b$

therefore

$$\begin{gathered} \cos (a+b)=\cos a\cos (-b)+\sin a\sin (-b) \\ \cos (a+b)=\cos a\cos b-\sin a\sin b \end{gathered}$$

Proving Sum and Difference of Sine Functions

Summing of sine functions

Draw a right-angled triangle ABC as shown below.

An image of a right triangle, - StudySmarter Originals

Draw another line intersecting A and touching line BC at D, such that angle BAD is β and angle DAC is α as seen below.

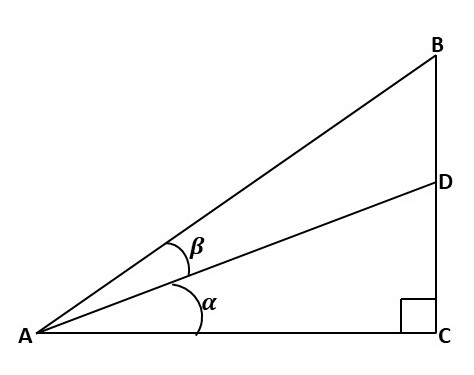
Draw a line perpendicular to point D which touches line AB at E as seen below.

Draw a line from point E which is perpendicular to line AC cuts through line AD at F and meets line AC at G as shown below.

Draw a line from point D to point H on the line EG which is perpendicular to line EG as seen below.

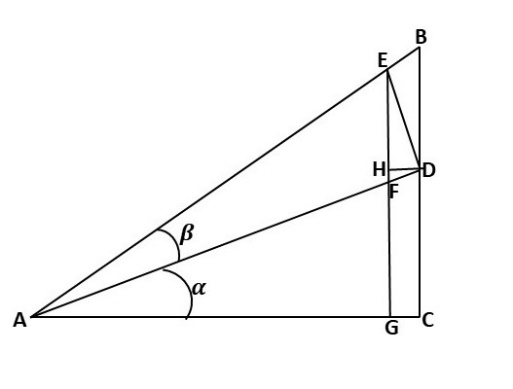
Note that for each step hereafter, you should refer to the figure above.

Therefore

Using SOHCAHTOA

$\sin (\alpha +\beta )=\frac{EG}{AE}$

Note that line EG = EH + HG, thus

$$\begin{gathered} \sin (\alpha +\beta )=\frac{EH+HG}{AE} \\ \sin (\alpha +\beta )=\frac{EH}{AE}+\frac{HG}{AE} \end{gathered}$$

Recall;

$HG=DC$

Thus

$\sin (\alpha +\beta )=\frac{EH}{AE}+\frac{DC}{AE}$

See that

$\angle DAC=\angle FDH$

Note below

$\angle DAC=\angle FDH=\alpha$

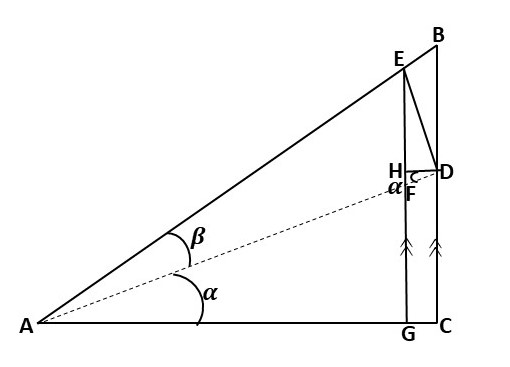
Recall that line AD is perpendicular to line ED. Therefore

$\angle HDE=90°-\alpha$

Knowing that

$\angle EHD=90°$

thus

$\angle HED+90°+90°-\alpha =180°$

$\angle HED+180°-180°=\alpha$

$\angle HED=\alpha$

Looking at their angles, it means that triangle ADC and EDH are similar. see below

An image that proves the summation of sine of angles, StudySmarter Originals

From the right-angled triangle EDH

$$\begin{gathered} \cos \alpha =\frac{EH}{ED} \\ EH=ED\cos \alpha \end{gathered}$$

Recall that

$\sin (\alpha +\beta )=\frac{EH}{AE}+\frac{DC}{AE}$

Substitute the value of EH

$$\begin{gathered} \sin (\alpha +\beta )=\frac{ED\cos \alpha }{AE}+\frac{DC}{AE} \\ \sin (\alpha +\beta )=(\frac{ED}{AE}\times \cos \alpha )+\frac{DC}{AE} \end{gathered}$$

Meanwhile, from the right-angled triangle AED, using SOHCAHTOA

$\sin \beta =\frac{ED}{AE}$

Substitute the value of $\frac{ED}{AE}$ in the equation

$\sin (\alpha +\beta )=\sin \beta \cos \alpha +\frac{DC}{AE}$

From the right-angled triangle ADC, using SOHCAHTOA

$$\begin{gathered} \sin \alpha =\frac{DC}{AD} \\ DC=AD\sin \alpha \end{gathered}$$

Substitute the value of DC in the equation

$\sin (\alpha +\beta )=\sin \beta \cos \alpha +\frac{AD\sin \alpha }{AE}$

Looking at the right-angled triangle AED and using SOHCAHTOA

$\cos \beta =\frac{AD}{AE}$

Substitute the value of$\frac{AD}{AE}$ in the equation

$$\begin{gathered} \sin (\alpha +\beta )=\sin \beta \cos \alpha +\cos \beta \sin \alpha \\ \sin (\alpha +\beta )=\sin \alpha \cos \beta +\sin \beta \cos \alpha \end{gathered}$$

Difference of its functions

Knowing that

$\sin (\alpha +\beta )=\sin \alpha \cos \beta +\sin \beta \cos \alpha$

Thus $\sin (\alpha -\beta )$ can be derived by exchanging β with -β throughout the equation.

Therefore

$\sin (\alpha -\beta )=\sin \alpha \cos (-\beta )+\sin (-\beta )\cos \alpha$

Note that

$\cos (-\beta )=\cos \beta$

and

$\sin (-\beta )=-\sin \beta$

therefore

$\sin (\alpha -\beta )=\sin \alpha \cos \beta -\sin \beta \cos \alpha$

Proving Sum and Difference of Tangent Functions

Summing of tangent functions

Recall that

$\tan \varnothing =\frac{\sin \varnothing }{\cos \varnothing }$

Therefore

$\tan (A+B)=\frac{\sin (A+B)}{\cos (A+B)}$

Thus

$\tan (A+B)=\frac{\sin A\cos B+\sin B\cos A}{\cos A\cos B-\sin A\sin B}$

Divide every entity of the right-hand side of the equation by cosAcosB

$$\begin{gathered} \tan (A+B)=\frac{\frac{\sin A\cos B}{\cos A\cos B}+\frac{\sin B\cos A}{\cos A\cos B}}{\frac{\cos A\cos B}{\cos A\cos B}-\frac{\sin A\sin B}{\cos A\cos B}} \\ \tan (A+B)=\frac{\tan A+\tan B}{1-\tan A\tan B} \end{gathered}$$

Difference of tangent functions

Recall that

$\tan \varnothing =\frac{\sin \varnothing }{\cos \varnothing }$

Therefore

$\tan (A-B)=\frac{\sin (A-B)}{\cos (A-B)}$

Thus

$\tan (A-B)=\frac{\sin A\cos B-\sin B\cos A}{\cos A\cos B+\sin A\sin B}$

Divide every entity of the right-hand side of the equation by cosAcosB

$$\begin{gathered} \tan (A-B)=\frac{\frac{\sin A\cos B}{\cos A\cos B}-\frac{\sin B\cos A}{\cos A\cos B}}{\frac{\cos A\cos B}{\cos A\cos B}+\frac{\sin A\sin B}{\cos A\cos B}} \\ \tan (A-B)=\frac{\tan A-\tan B}{1+\tan A\tan B} \end{gathered}$$

Sum and difference of formulas application

Below you shall see how to apply the sum and difference formulas.