Triangle Rules: Trigonometry & Angles, Area

Jump to a key chapter

The triangle rules discussed in this article will explore this question in further detail:

Triangle rules – sine rule

The first triangle rule that we will discuss is called the sine rule. The sine rule can be used to find missing sides or angles in a triangle.

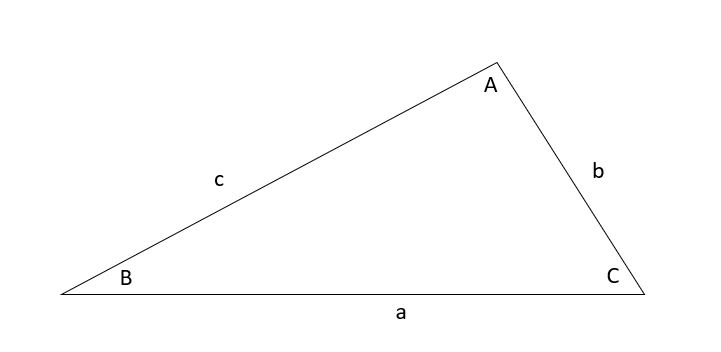
Consider the following triangle with sides a, b and c, and angles, A, B and C.

Triangle sine rule - StudySmarter Triangle with sides a, b and c, and angles, A, B and C, Nilabhro Datta - StudySmarter Originals

There are two versions of the sine rule.

For the above triangle, the first version of the sine rule states:

$\frac{a}{\sin (A)} = \frac{b}{\sin (C)} = \frac{c}{\sin (C)}$

This version of the sine rule is usually used to find the length of a missing side.

The second version of the sine rule states:

$\frac{\sin (A)}{a} = \frac{\sin (B)}{b} = \frac{\sin (C)}{c}$

This version of the sine rule is usually used to find a missing angle.

For the following triangle, find a.

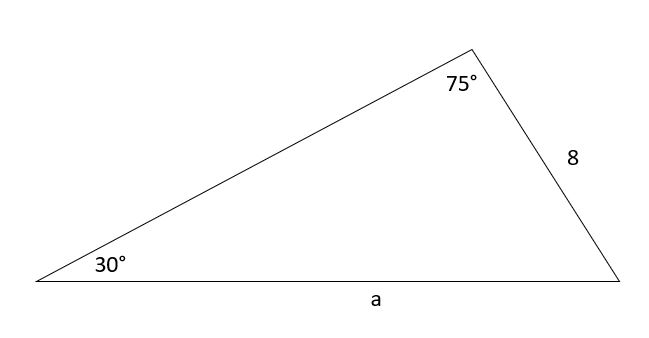
Triangle Rules Finding the length of a side StudySmarter

Solution

According to the sine rule,

$\frac{a}{\sin (A)} = \frac{b}{\sin (B)} \frac{a}{\sin (75)} = \frac{8}{\sin (30)} \frac{a}{0.966} = \frac{8}{0.5} a = 15.455$

Read Sine and Cosine Rules to learn about the sine rule in greater depth.

For this triangle, find x.

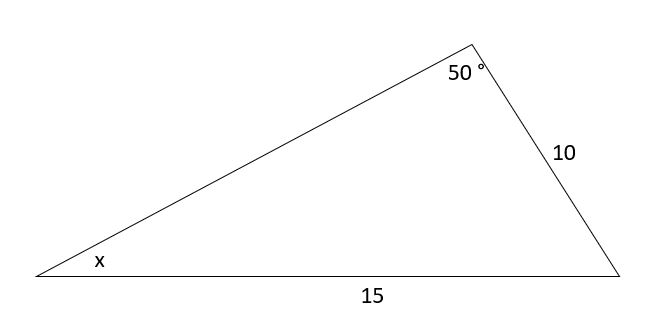
Triangle Rules Finding an angle StudySmarter

Solution

According to the sine rule,

$\frac{\sin (A)}{a} = \frac{\sin (B)}{b} \frac{\sin (x)}{10} = \frac{\sin (50)}{15} \frac{\sin (x)}{10} = \frac{0.766}{15} \Rightarrow x = 30.71 °$

Triangle rules – cosine rule

The second triangle rule that we will discuss is called the cosine rule. The cosine rule can be used to find missing sides or angles in a triangle.

Consider the following triangle with sides a, b and c, and angles, A, B and C.

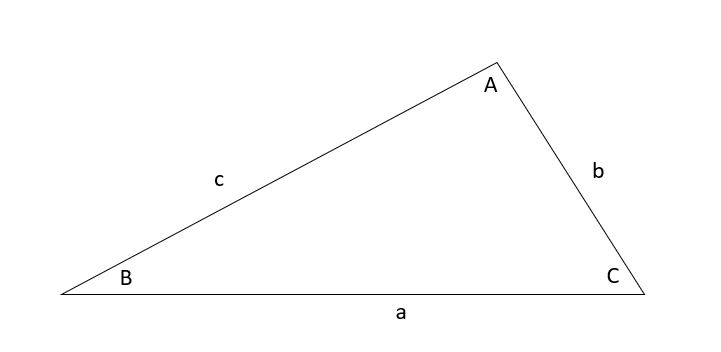
Triangle sine rule - StudySmarter

Triangle with sides a, b and c, and angles, A, B and C, Nilabhro Datta - StudySmarter Originals

There are two versions of the cosine rule.

For the above triangle, the first version of the cosine rule states:

a² = b² + c² - 2bc · cos (A)

This version of the cosine rule is usually used to find the length of a missing side when you know the lengths of the other two sides and the angle between them.

The second version of the cosine rule states:

$\cos (A) = \frac{b ² + c ² - a ²}{2 b c}$

This version of the cosine rule is usually used to find an angle when the lengths of all three sides are known.

Find x.

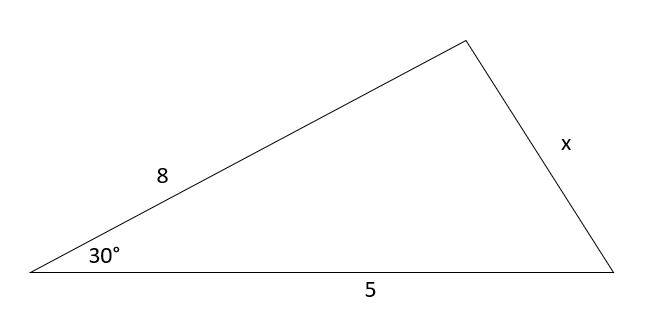
Triangle Rules Finding the length of a side StudySmarter

Solution

According to the cosine rule,

a² = b² + c² - 2bc · cos (A)

=> x² = 5² + 8² - 2 x 5 x 8 x cos (30)

=> x² = 19.72

=> x = 4.44

For the next triangle, find angle A.

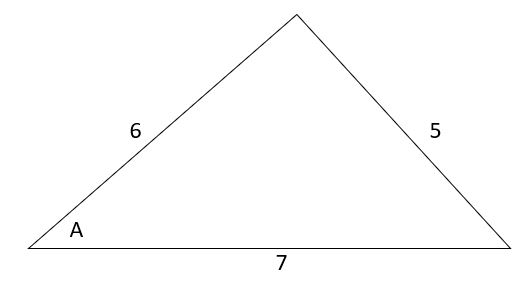
Triangle Rules Finding an angle StudySmarter

Solution

According to the cosine rule,

$\cos (A) = \frac{b ² + c ² - a ²}{2 b c} \Rightarrow \cos (A) = \frac{7^{2} + 6^{2} - 5^{2}}{2 \cdot 7 \cdot 6} \Rightarrow \cos (A) = \frac{5}{7} \Rightarrow A = 44.4 °$

Read Sine and Cosine Rules to learn about the cosine rule in greater depth.

Triangle Rules – the area of a triangle

We are already familiar with the following formula:

$A r e a o f a t r i a n g l e = \frac{1}{2} \cdot b a s e \cdot h e i g h t$

But what if we do not know the exact height of the triangle? We can also find out the area of a triangle for which we know the length of any two sides and the angle between them.

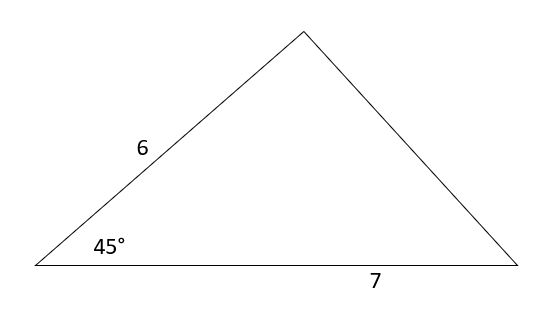
Consider the following triangle:

Triangle Rules area of a triangle sine rule StudySmarter

The area of the above triangle can be found by using the formula:

$A r e a = \frac{1}{2} a b \cdot \sin (C) = \frac{1}{2} b c \cdot \sin (A) = \frac{1}{2} a c \cdot \sin (B)$

Find the area of the triangle.

Triangle Rules area of a triangle sine rule StudySmarter

Solution

$A r e a = \frac{1}{2} a b \cdot \sin (C) = \frac{1}{2} \cdot 6 \cdot 7 \cdot \sin (45) = 14.85$

The area of the triangle is 10 Units. Find the angle x.

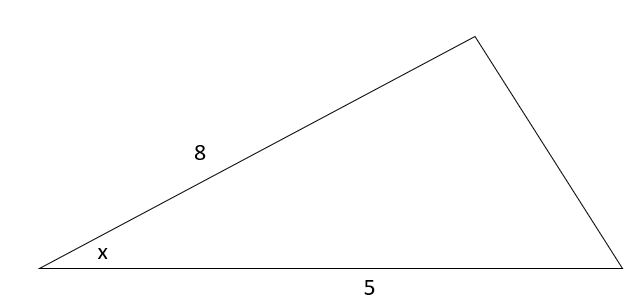
Triangle Rules Finding an angle StudySmarter

Solution

$A r e a = \frac{1}{2} a b \cdot \sin (C) \Rightarrow 10 = \frac{1}{2} \cdot 5 \cdot 8 \cdot \sin (x) \Rightarrow \sin (x) = 0.5 \Rightarrow x = 30 °$

Click on Area of Triangles to learn about the area of triangles rule in greater depth.

Triangle rules – key takeaways

You can use the sine rule to find missing sides or angles in a triangle.
The first version of the sine rule states that: $\frac{a}{\sin (A)} = \frac{b}{\sin (C)} = \frac{c}{\sin (C)}$ The second version of the sine rule states that $\frac{\sin (A)}{a} = \frac{\sin (B)}{b} = \frac{\sin (C)}{c}$
You can use the cosine rule to find missing sides or angles in a triangle.
The first version of the cosine rule states that:a² = b² + c² - 2bc · cos (A) The second version of the sine rule states that: $\cos (A) = \frac{b ² + c ² - a ²}{2 b c}$
We can find out the area of a triangle for which we know the length of any two sides and the angle between them using the following formula: $A r e a = \frac{1}{2} a b \cdot \sin (C) = \frac{1}{2} b c \cdot \sin (A) = \frac{1}{2} a c \cdot \sin (B)$

Already have an account? Log in

Frequently Asked Questions about Triangle Rules

What is the sine rule for triangles?

The sine rule for triangles states that

a/sin(A)=b/sin(B)=c/sin(C)

How do you calculate area of a triangle using the sine rule?

The sine rule can be used to find find missing sides or angles in a triangle. Once we have sufficient information, we can used the formula Area=1/2*a*b*sin(C)

Can the sine rule be used with right-angled triangles?

Yes, in that case, one of the angles will be 90.

Save Article

Discover learning materials with the free StudySmarter app

About StudySmarter

StudySmarter is a globally recognized educational technology company, offering a holistic learning platform designed for students of all ages and educational levels. Our platform provides learning support for a wide range of subjects, including STEM, Social Sciences, and Languages and also helps students to successfully master various tests and exams worldwide, such as GCSE, A Level, SAT, ACT, Abitur, and more. We offer an extensive library of learning materials, including interactive flashcards, comprehensive textbook solutions, and detailed explanations. The cutting-edge technology and tools we provide help students create their own learning materials. StudySmarter’s content is not only expert-verified but also regularly updated to ensure accuracy and relevance.

Learn more

StudySmarter Editorial Team

Team Math Teachers

5 minutes reading time
Checked by StudySmarter Editorial Team

Save Explanation

Triangle Rules

StudySmarter Editorial Team

Triangle rules – sine rule

Solution

Solution

Triangle rules – cosine rule

Solution

Solution

Triangle Rules – the area of a triangle

Solution

Solution

Triangle rules – key takeaways

Learn faster with the 0 flashcards about Triangle Rules

Frequently Asked Questions about Triangle Rules

Discover learning materials with the free StudySmarter app

About StudySmarter

StudySmarter Editorial Team

Study anywhere. Anytime.Across all devices.

Company

Product

Help

Triangle Rules

StudySmarter Editorial Team

Triangle rules – sine rule

Solution

Solution

Triangle rules – cosine rule

Solution

Solution

Triangle Rules – the area of a triangle

Solution

Solution

Triangle rules – key takeaways

Learn faster with the 0 flashcards about Triangle Rules

Frequently Asked Questions about Triangle Rules

Discover learning materials with the free StudySmarter app

About StudySmarter

StudySmarter Editorial Team

Study anywhere. Anytime.Across all devices.

Create a free account to save this explanation.

Join over 22 million students in learning with our StudySmarter App