What is the main set of trigonometric identities?
There are two main formulaic identities that must be learnt to prove and solve other Equations. These are:
 and
and
Let’s prove these identities starting with .
Proof:
Firstly let’s draw a triangle with angle θ.
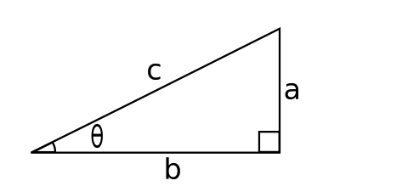
General Triangle of angle θ
Now if we write out expressions for a and b using SOHCAHTOA we get:
Therefore:
Now if we square both of these expressions for sin and cos we get:
Summing these we get:
By Pythagoras' theorem:
Therefore:
Now let’s move on to proving . The first half of this Proof is identical to the Proof above.
PROOF:
Firstly let’s draw a triangle with angle θ.
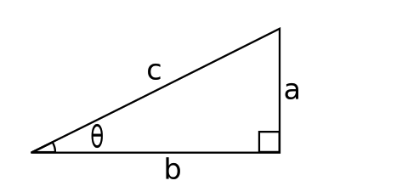
Now if we write out expressions for a and b using SOHCAHTOA we get:
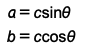
So
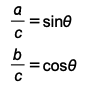
Now if we divide these two expressions for sin and cos:
This is an expression for the opposite side over the adjacent side, therefore:
Therefore:
Now let’s look at some worked examples where trigonometric identities can be applied.
Worked examples using trigonometric identities
Solve the equation for
SOLUTION:The first thing to do would be to substitute
for
.The equation now ends up being
.Simplifying this further:
Now we can solve this like a quadratic by taking
.
Now we need to do x = cos
-1(y)We can only perform cos
-1(0.5)=60°This is because 1.5 > 1 so we cannot perform a cos
-1 function of this.So the only answer is 60°.
Let's look at another example of rearranging trigonometric identities.
Show that the equation can be written as
SOLUTION:Firstly let’s rearrange to get rid of any denominators.
Now let’s replace
with
:
Now get rid of the denominator by multiplying through by
:
Now replace
with
:
Now rearrange this equation:
QED
What other trigonometric identities can we derive?
Firstly we need to know three new bits of terminology:
These are all reciprocals of standard sin, cos and tan.
Deriving new identities
Now let’s look at the identity :
If we divide the entire equation by
we get:
Now using the identity
:
This is our first new identity. Now if we divide our entire equation by
Now using the identity
, so :
Now we have our two new identities:
Let’s see them in action in some worked examples.
Worked examples of new identities
Solve, for 0 ≤ θ < 360°, the equation:
to 1 dp.

 Graph of y=cosx. Image: Ruben Verhaegh, CC BY-SA 4.0
Graph of y=cosx. Image: Ruben Verhaegh, CC BY-SA 4.0
We can see that if we perform the identity , the other value of is .
Then we need to perform , again using the identity , .
So to 1 decimal place our 4 solutions in degrees are:
Trigonometric Identities - Key takeaways
Trigonometric identities are used to derive new formulae and equations.
They can help solve equations involving Trigonometry.
They help us geometrically visualise real-life situations.
They have proofs, which can be adapted from basic Trigonometry.
Images:
Graph of y=cos x: https://commons.wikimedia.org/wiki/File:Cos(x).PNG




 and
and 
 Now if we write out expressions for a and b using SOHCAHTOA we get:
Now if we write out expressions for a and b using SOHCAHTOA we get: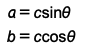 So
So 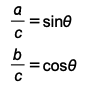 Now if we divide these two expressions for sin and cos:
Now if we divide these two expressions for sin and cos:




