What are 2D and 3D vectors?
Now we know what a vector quantity is, how does that relate to maths? Let's first think about how a vector would look in two dimensions. Usually, in two dimensions, we describe things using an x-coordinate and a y-coordinate, as this can describe any point in the xy-plane. By doing this, we describe how far we move in the x direction and then how far we move in the y direction, meaning we have satisfied our need for magnitude and direction.
We can write this vector in a couple of ways. The most common way is as a column vector. In 2D, this looks like  , where x corresponds to the x coordinate and y to the y coordinate. We can also write a vector using unit vectors. In 2D, our unit vectors are represented by i and j , where i is one unit in the x direction, and j is one unit in the y direction. This means that we can write
, where x corresponds to the x coordinate and y to the y coordinate. We can also write a vector using unit vectors. In 2D, our unit vectors are represented by i and j , where i is one unit in the x direction, and j is one unit in the y direction. This means that we can write  = x i + y j .
= x i + y j .
By definition, we take a positive x value in our vector to mean going to the right of the origin. Conversely, a negative x value represents going to the left of the origin. Again, by definition, we take a positive y value to mean pointing upwards from the origin, and conversely, a negative y value represents going down from the origin.
For example, if I want to show the vector  on a coordinate axis, it would be as shown below.
on a coordinate axis, it would be as shown below.
 Plotting a vector on a graph
Plotting a vector on a graph
Notice here that to show the vector  , I have shown the vector
, I have shown the vector first and then the vector
first and then the vector  . It is important to note that whenever we are drawing vectors, we must draw on an arrow to show the direction of the vector. Without this, we wouldn't be able to identify the vector
. It is important to note that whenever we are drawing vectors, we must draw on an arrow to show the direction of the vector. Without this, we wouldn't be able to identify the vector  from the vector
from the vector  . When we write a vector going from, eg point A to point B, we denote this vector
. When we write a vector going from, eg point A to point B, we denote this vector  . If it were to go the other way, it would be called
. If it were to go the other way, it would be called  . Note that the arrow shows the direction of travel.
. Note that the arrow shows the direction of travel.
We can extend this thinking to three dimensions. In the z-direction, the unit vector is denoted by k . This looks like  in column vector form. A three-dimensional axis looks like this:
in column vector form. A three-dimensional axis looks like this:
 Plotting a three-dimensional vector
Plotting a three-dimensional vector
The thing to remember is that all three axes are perpendicular to each other. (If your tabletop were the xy plane, the z-direction would be coming directly out from the table.) If we had a vector of the form r =  , we could express it as r = x i + y j + z k in terms of unit vectors.
, we could express it as r = x i + y j + z k in terms of unit vectors.
Calculating the magnitudes and directions of vectors
When looking at vectors, we can also directly describe their magnitude and direction. However, it is not obvious how to relate what we see geometrically to the ideas of magnitude and direction. We will explore this further now.
Magnitude
Visually, the magnitude of a vector is its length. We can show the magnitude of vector a as | a |.
Let's first think about this in two dimensions, and then we can extend these ideas to three dimensions. In 2D, we can draw a right-angled triangle around our vector, using the vector itself as the hypotenuse of the triangle. This Means we can use Pythagoras' Theorem to find the formula for a vector in 2D:  .
.
A sketch of the vector and the triangle are shown below.
 Calculating a vector using a right-angled triangle
Calculating a vector using a right-angled triangle
We now need to extend this idea to three dimensions. As before, we need to add the z term to the 2D formula, and so the formula in three dimensions is 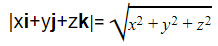
Find the magnitude of the vector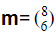
Using the formula for magnitude, we get 
Find the magnitude of the vector  .
.
Using the formula for magnitude, we get
The direction of a vector
We measure the direction of a vector with respect to another point. In two dimensions, this is usually the x-axis, but we always need to specify. Let's draw a diagram to explain this better.
 Measuring the direction of a vector
Measuring the direction of a vector
We give directions in terms of  , so this means that in two dimensions, the direction of any vector
, so this means that in two dimensions, the direction of any vector with respect to the x-axis is given as
with respect to the x-axis is given as . If we wanted to measure the angle with respect to the y-axis, this would be given as
. If we wanted to measure the angle with respect to the y-axis, this would be given as  . Notationally, we take anything above the x-axis as a positive value of theta, and anything below the axis will give a negative value of theta.
. Notationally, we take anything above the x-axis as a positive value of theta, and anything below the axis will give a negative value of theta.
We can extend this to any axis in three dimensions. Suppose we have a vector  , and we want to find the angle with each axis. The formulas are given as follows:
, and we want to find the angle with each axis. The formulas are given as follows:
Find the direction of a = 3 i - 2 j + 2 k with respect to the x-axis.
First, let's work out | a | :  . Then by the formula, the angle with the x-axis is given by
. Then by the formula, the angle with the x-axis is given by  , which gives
, which gives  .
.
Adding and subtracting vectors
Some calculations require you to add and subtract vectors.
Vector addition
How do we add two vector quantities together? Let's first think of this geometrically. To add two vectors together, we would draw our first vector as usual, starting from the origin. We would then draw the second vector starting at the end of our first vector. We would then draw a line from the origin to the end of the second vector to get the result of adding the two vectors. This new vector is called the resultant vector . This process is shown below.
 Adding vectors
Adding vectors
Now we know how to do this geometrically. What is the process algebraically? It turns out that we can add two vectors simply by adding the corresponding components. This means that the formula for adding two vectors is given by  in two dimensions. The process is exactly the same in three dimensions.
in two dimensions. The process is exactly the same in three dimensions.
Add the vectors  and
and  .
.
Using the formula, we get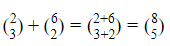
Add the vectors  and
and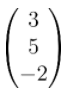
We can add components to get 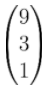
Vector subtraction
This is very similar both geometrically and algebraically. Geometrically, when we take away a vector, we reverse its direction and then follow the same process. Algebraically, we take away components, so for two vectors, we get
 . Again, the process is exactly the same in three dimensions.
. Again, the process is exactly the same in three dimensions.
Calculate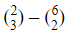
Using the given formula, we get 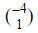
Calculate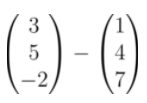
Subtraction elementwise gives us 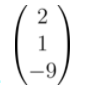
Finding the distance between two vector position points
Suppose we are given two points in vector form  and
and  , and we wish to find the direct distance between these points. We could find a vector connecting these two points by taking one vector away from the other. We have the distance between the points as a vector, so we now need to find the length of the vector. This is given by the magnitude of this vector.
, and we wish to find the direct distance between these points. We could find a vector connecting these two points by taking one vector away from the other. We have the distance between the points as a vector, so we now need to find the length of the vector. This is given by the magnitude of this vector.
How do you do geometric proofs with vectors?
You might be asked about geometric Proof with vectors. This type of question will typically look like a shape annotated with vector lengths. It will ask us to show something - the length of a certain side as a combination of the given lengths, proving two sides are parallel or perpendicular, or proving midpoints. These are best shown through examples.
 Vector geometric Proof question 1
Vector geometric Proof question 1
P is a point on AB such that AP: PB = 1: 3
Show that  is
is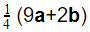
To find  we can break this down to
we can break this down to  .
.
 , and we can break
, and we can break  down as
down as  .
.
This means that  .
.
Thus, \[
\vec{OP} = \vec{OA} + \vec{AP} = 3a + \frac{1}{4}(2b - 3a) = \frac{9}{4}a + \frac{1}{2}b = \frac{1}{4}(9a + 2b)
\]
 Vector geometric proof question 2
Vector geometric proof question 2
C is a point on AO such that AC: CO = 3: 1
M and N are the midpoints of BC and BO respectively
Let us denote by a and
by a and  by b.
by b.
Show that MN is parallel to AO.
 , so we need to show MN is k a for any constant k.
, so we need to show MN is k a for any constant k.
 , by breaking it down.
, by breaking it down.
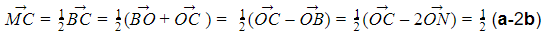
 .
.This means we can write  , which satisfies what we needed to show. QED
, which satisfies what we needed to show. QED
What type of physical quantities are vectors?
Now we've seen the mathematical interpretation of vectors, how do we apply these to real life? We've already discussed velocity being a vector quantity. When we describe velocity, we give the magnitude (commonly known as speed in this context) and the direction of travel. Position, velocity and acceleration are all vector quantities related to each other (velocity is the rate of change of position, and acceleration is the rate of change of velocity).
Forces are also a vector quantity, as the direction and magnitude of the force matter. This means that quantities such as thrust, weight and momentum are also vector quantities.
Applications of vector problems
We can apply our knowledge of vectors to other types of questions, too. Examples would include finding the position vector of a missing vertex of a shape or translating a shape by a vector. Let's look at how to calculate these.
Translate the rectangle given by (0,0), (4,7), (4,0), (0,7) by the vector  .
.
Visually, this looks like moving the shape one unit in the positive x direction and four Units in the positive y direction. To find the coordinates of the translated rectangle, we would need to add the vector to each position vector of a corner, which would give us (1, 4), (5, 11), (5, 4 ), (1, 11).
Note: We switch between coordinates and position vectors freely here, as they represent the same thing for our purposes.
A parallelogram has given vertices  . Find the missing vertex.
. Find the missing vertex.
The best place to start here is by plotting points. This gives us Finding the missing vertex of a shape
Finding the missing vertex of a shape
For the completed shape to be a parallelogram, we need the y coordinate to be 4. Then we can find the x coordinate by finding the difference of x between (1, 1) and (8, 1) and adding it to the x value of the top point (shown in black). This gives us 7, meaning that the x coordinate is 10, giving the final point as  .
.
Vectors - Key takeaways
i , j , k are the unit vectors in the x, y and z directions, respectively.
A vector has direction and magnitude.
The magnitude of a vector is given by the square root of the sum of the components of the vector squared.
Vector addition, subtraction and scalar multiplication occur elementwise.




 , where x corresponds to the x coordinate and y to the y coordinate. We can also write a vector using unit vectors. In 2D, our unit vectors are represented by i and j , where i is one unit in the x direction, and j is one unit in the y direction. This means that we can write
, where x corresponds to the x coordinate and y to the y coordinate. We can also write a vector using unit vectors. In 2D, our unit vectors are represented by i and j , where i is one unit in the x direction, and j is one unit in the y direction. This means that we can write  = x i + y j .
= x i + y j .  on a coordinate axis, it would be as shown below.
on a coordinate axis, it would be as shown below.
 , I have shown the vector
, I have shown the vector first and then the vector
first and then the vector  . It is important to note that whenever we are drawing vectors, we must draw on an arrow to show the direction of the vector. Without this, we wouldn't be able to identify the vector
. It is important to note that whenever we are drawing vectors, we must draw on an arrow to show the direction of the vector. Without this, we wouldn't be able to identify the vector  from the vector
from the vector  . When we write a vector going from, eg point A to point B, we denote this vector
. When we write a vector going from, eg point A to point B, we denote this vector  . If it were to go the other way, it would be called
. If it were to go the other way, it would be called  . Note that the arrow shows the direction of travel.
. Note that the arrow shows the direction of travel. in column vector form. A three-dimensional axis looks like this:
in column vector form. A three-dimensional axis looks like this:
 , we could express it as r = x i + y j + z k in terms of unit vectors.
, we could express it as r = x i + y j + z k in terms of unit vectors. .
.
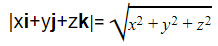
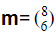

 .
.

 , so this means that in two dimensions, the direction of any vector
, so this means that in two dimensions, the direction of any vector with respect to the x-axis is given as
with respect to the x-axis is given as . If we wanted to measure the angle with respect to the y-axis, this would be given as
. If we wanted to measure the angle with respect to the y-axis, this would be given as  . Notationally, we take anything above the x-axis as a positive value of theta, and anything below the axis will give a negative value of theta.
. Notationally, we take anything above the x-axis as a positive value of theta, and anything below the axis will give a negative value of theta. , and we want to find the angle with each axis. The formulas are given as follows:
, and we want to find the angle with each axis. The formulas are given as follows:


 . Then by the formula, the angle with the x-axis is given by
. Then by the formula, the angle with the x-axis is given by  , which gives
, which gives  .
.
 in two dimensions. The process is exactly the same in three dimensions.
in two dimensions. The process is exactly the same in three dimensions. and
and  .
.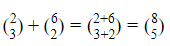
 and
and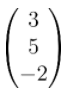
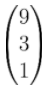
 . Again, the process is exactly the same in three dimensions.
. Again, the process is exactly the same in three dimensions.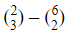
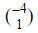
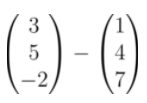
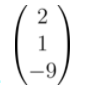
 . Geometrically, we can see this as the vector
. Geometrically, we can see this as the vector  joined to itself over and over a times. This means that for any non-zero a,
joined to itself over and over a times. This means that for any non-zero a, is parallel to
is parallel to . Algebraically, this means that
. Algebraically, this means that . Again, we can follow the process for three dimensions.
. Again, we can follow the process for three dimensions.

 and
and  , and we wish to find the direct distance between these points. We could find a vector connecting these two points by taking one vector away from the other. We have the distance between the points as a vector, so we now need to find the length of the vector. This is given by the magnitude of this vector.
, and we wish to find the direct distance between these points. We could find a vector connecting these two points by taking one vector away from the other. We have the distance between the points as a vector, so we now need to find the length of the vector. This is given by the magnitude of this vector. and
and  .
. and
and  . We do this by taking away one vector from the other
. We do this by taking away one vector from the other  . We now need to find the magnitude of this vector. This is given by
. We now need to find the magnitude of this vector. This is given by  - which is our answer.
- which is our answer.
 is
is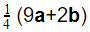
 we can break this down to
we can break this down to  .
. , and we can break
, and we can break  down as
down as  .
. .
.
 by a and
by a and  by b.
by b. , so we need to show MN is k a for any constant k.
, so we need to show MN is k a for any constant k. , by breaking it down.
, by breaking it down.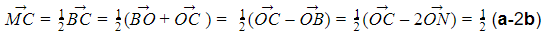
 .
. , which satisfies what we needed to show. QED
, which satisfies what we needed to show. QED .
. . Find the missing vertex.
. Find the missing vertex.
 .
.


