The making of astronomical telescopes is a very old discipline. In the seventeenth century, Galileo Galilei became the first person to point a telescope towards the sky. His own telescope was able to magnify objects by up to twenty times, which allowed him to observe distant objects with his eyes. Nowadays, telescopes do not require us to look with our eyes because machines can gather data more precisely than we do (digital astronomical telescopes). Also, if we only observe with our eyes, we are limited to measurements in the visible region of the electromagnetic spectrum.
Despite this, it is still relevant to study how telescopes (based on the first design by Galileo) function to understand how the magnification of other telescopes works.
How do lenses work?
Before we look at how telescopes allow us to magnify distant objects, we need to understand the basic operation of lenses.
A lens is an optical, physical device that focuses or disperses light due to refraction.
A lens is characterised by its focal distance. The position of objects in relation to this distance determines what happens with the rays of light that are refracted by the lens.
The focal distance is the distance at which we can place an object to form its image at an infinite distance.
There are two main types of lenses: converging and diverging. While the first kind focuses the incident light towards a point, the latter disperses it. In this explanation, we are only concerned with converging lenses since these are the ones that can be used to build the simplest model of an astronomical telescope.
Below we look at the diagrammatic functioning of converging lenses and their mathematical description to understand the power of the amplification of telescopes.
Diagrams of converging lenses
See the two images below:
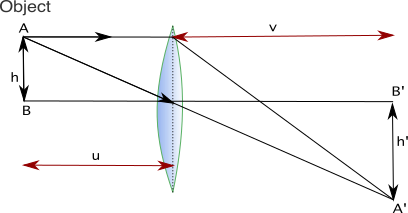
Figure 1. Formation of a real image by a converging lens, Manuel R. Camacho – StudySmarter Originals
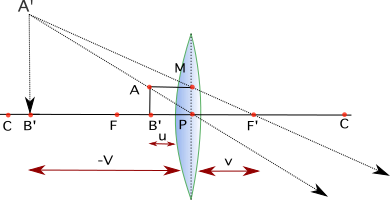
Figure 2. Formation of a virtual image by a converging lens, Manuel R. Camacho – StudySmarter Originals
These diagrams summarise the possible images formed with a converging lens. Here are the basic rules to construct these diagrams:
- Draw the object on one side of the lens (choice is arbitrary, we chose left).
- Draw the lens and mark its focal distance as f. The distances do not have to correspond to the real distance, but you do need to choose a scale so that the relation between the focal distance and the object’s distance to the lens is proportional to the real one.
- A ray travels horizontally from the object to the lens and, after being refracted by the lens, travels to a point on the horizontal middle line that is a focal distance away from the lens (focal point F).
- A ray travels from the object and crosses the lens through its middle point. This ray is not refracted and continues undisturbed.
- If the solid lines do not cross on the right of the lens, you need to extend them to the left (denoted by the dashed line) in order for the lines to cross and form a virtual image
By following these simple rules, we can find the two rays with undotted lines in the images above. It is important to note that the formation of the image depends on the object’s position with respect to the focal point of the lens.
- If the object is beyond the focal point, the light rays meet on the other side of the lens and an image is formed there. This image is turned upside down. The image will be bigger if the object is placed at less than twice the focal distance. If it is beyond that distance, the image will be smaller.
- If the object is between the focal point and the lens, the undotted light rays do not meet on the other side of the lens. By continuing the lines with the dotted lines as shown in figure 2, we can see that the image is formed on the same side of the lens where the object is. The image has the same orientation as the object and is always bigger than the object.
- If the object is on the focal point, the image is formed on the other side of the lens at an infinite distance with the same size.
When an image of an object is formed on the opposite side of a lens, the image can be projected on a screen. These images are called real images. When an image of an object is formed on the same side of a lens, the image cannot be projected on a screen, but it is observed where it forms. These images are called virtual images.
- Real image = image formed on the opposite side of a lens
- Virtual image = image formed on the same side of a lens
Mathematical description of converging lenses
Converging lenses obey the following equation:
\[\frac{1}{x_0} + \frac{1}{x_i} = \frac{1}{f}\]
Here, xo is the distance of the object to the lens, f is the focal distance of the lens, and xi is the distance of the image of the object. We always take xo to be positive, so if xi is negative, it will be a virtual image, and if xi is positive, it will be a real image.
- If xi is negative = virtual image
- If xi is positive = real image
Since lenses are considered ideal systems, there is also a straightforward relationship between the vertical size and the horizontal distances. This translates into the fact that the magnification of lenses (the amount of growth of the image of an object with respect to its actual size) follows this equation:
\[M = \frac{y_i}{y_o} = \Big|\frac{x_i}{x_0} \Big|\]
Here, yi is the vertical size of the image, yo is the vertical size of the object, and the absolute value appears because we take magnification to be a positive quantity. The absolute value indicates the amount of growth, and the sign indicates whether the orientation of the image is the same as the object’s or if it is the opposite.
Take a converging lens whose focal distance f is 10cm. Calculate the characteristics of the image of an object if it is placed at:
a) 15cm from the lens.
We can calculate the distance where the image is produced by applying the formula for converging lenses:
\(\frac{1}{x_0} + \frac{1}{x_i} = \frac{1}{f} \rightarrow x_i = \frac{1}{\frac{1}{f} - \frac{1}{x_0}} = \frac{1}{\frac{1}{10cm} - \frac{1}{15cm}} = 30 cm\)
Since the quantity is positive, the image is formed on the opposite side of the lens and upside down (as we know from the first diagram). We can now calculate the magnification:
\(M = \frac{y_i}{y_0} = \Big| \frac{x_i}{x_0} \Big| = \Big|\frac{30 cm}{15cm} \Big| = 2\)
This means that the image produced is double the size of the object.
b) 30cm from the lens
We can calculate the distance where the image is produced by applying the formula for converging lenses:
\(\frac{1}{x_0} + \frac{1}{x_i} = \frac{1}{f} \rightarrow x_i = \frac{1}{\frac{1}{f} - \frac{1}{x_0}} = \frac{1}{\frac{1}{10 cm} - \frac{1}{30 cm}} = 15 cm\)
Since the quantity is positive, the image is formed on the opposite side of the lens and upside down. We can calculate the magnification as
\(M = \frac{y_i}{y_0} = \Big|\frac{x_i}{x_0} \Big| = \Big| \frac{15 cm}{30 cm} \Big| = 0.5\)
This means that the image produced is half the size of the object.
c) 5cm from the lens.
We can calculate the distance where the image is produced by applying the formula for converging lenses:
\(\frac{1}{x_0} + \frac{1}{x_i} = \frac{1}{f} \rightarrow x_i = \frac{1}{\frac{1}{f} - \frac{1}{x_0}} = \frac{1}{\frac{1}{10 cm} - \frac{1}{5 cm}} = -10 cm\)
Since the quantity is negative, the image is formed on the same side of the lens and upright (as we know from the second diagram). We can calculate the magnification as
\(M = \frac{y_i}{y_0} = \Big|\frac{x_i}{x_0} \Big| = \Big| \frac{-10 cm}{5 cm} \Big| = 2\)
This means that the image produced is double the size of the object.
What is an astronomical refracting telescope?
Telescopes have been used since Galileo’s invention to explore the universe. Galileo’s first design used the combined refraction of two lenses to amplify images, but there have been many developments since then to enhance the observation properties of these devices. Nevertheless, the study of simple refracting telescopes provides a good understanding of the general functioning of telescopes.
Definition and characteristics of an astronomical telescope of two lenses
A two-lens astronomical refracting telescope is a device that magnifies the images of distant objects by combining two converging lenses one after the other.
These two lenses (the objective lens and eyepiece lens) fulfil different roles, and their combination allows us to use telescopes as powerful observation tools.
- The objective lens collects the incident light and creates an image by focusing light. Ideally, it should be very large to collect more light (more resolution and intensity), and it should have a considerable focal distance.
- The eyepiece lens magnifies the image and creates a virtual image at infinity so that it can be seen by an observer. It should have a small focal distance.
Below is a diagram of the disposition of the two lenses and how rays of light are refracted.
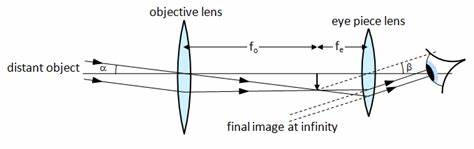
Two-lens astronomical refracting telescope, Keith Gibbs School
PhysicsThe angles α and β are very small for astronomical observations, so they can be neglected. In the image, fo is the focal distance of the objective lens, and fe is the focal distance of the eyepiece lens. The distance between the lenses has to be the sum of their focal distances so that the virtual image is formed at an infinite distance.
Astronomical telescope magnification and formula derivation
Finally, let’s investigate how powerful astronomical telescopes are. For a telescope, the usual calculations with lenses do not yield helpful information because we are working with objects so far away that we can consider their light rays to be parallel. Furthermore, we are also working with images that are placed exactly at the focal point of a lens.
As we only offer a simplified version of lenses in the first sections, we apply these general ideas to obtain the magnification. Since magnification is the ratio of the size of the image to the actual object, we can obtain this information by using the angles α and β. It turns out that for astronomical measurements, these angles have the following expressions:
\[\alpha = \frac{\gamma}{f_e} \qquad \beta = \frac{\gamma}{f_e}\]
To find the ratio of the sizes of the image of the object and the image we observe, we have to divide the two angles, which yields:
\[M = \Big| \frac{\alpha}{\beta} \Big| = \frac{f_0}{f_e}\]
We can now see why it is useful that the objective lens has a very large focal distance and the eyepiece lens has a small focal distance.
If we have a telescope whose objective lens has a focal distance of 1m and whose eyepiece lens has a focal distance of 1mm, the magnification is 1000. This is the power of telescopes, and they can be made of more complex combinations of lenses to increase their power even.
Astronomical Telescopes - Key takeaways
- An astronomical telescope is a device that allows us to gather data on very distant objects in the universe.
- Optical telescopes are based on the refractive properties of lenses. Galileo Galilei created the first optical telescope.
- The most basic model of a telescope is made of two converging lenses combined in a specific way.
- The magnification power is the amount of growth of the image observed with respect to the received image.
- The whole functioning of lens-based refracting telescopes is based on the laws of optics that govern how lenses deviate light rays.
ImagesRefracting telescopes – telescopes using large lenses for their objective. https://www.schoolphysics.co.uk/age16-19/Optics/Optical%20instruments/text/Telescopes_/index.html










