Although both gases and liquids are fluids, there are differences between them. First, liquids are incompressible, while gases are highly compressible. And secondly, the intermolecular forces in between gases are nearly non-existent, allowing them to move freely. Liquids, by contrast, have stronger forces binding them together.
These characteristics make gases perfect for transmitting and generating work. In some applications, gases don’t flow or are forced into rigid chambers, as in combustion chambers, Stirling engines, or pneumatic devices. In these devices, heat is exchanged, and the volume and pressure might vary as well. In these processes, the fluids are modelled as those in which there is no flow.
Non-flow processes
In thermodynamics engineering, any processes in which gases do not flow past a boundary are known as non-flow or closed-system processes, in which the gas volume is considered to be fixed. See the illustration below:
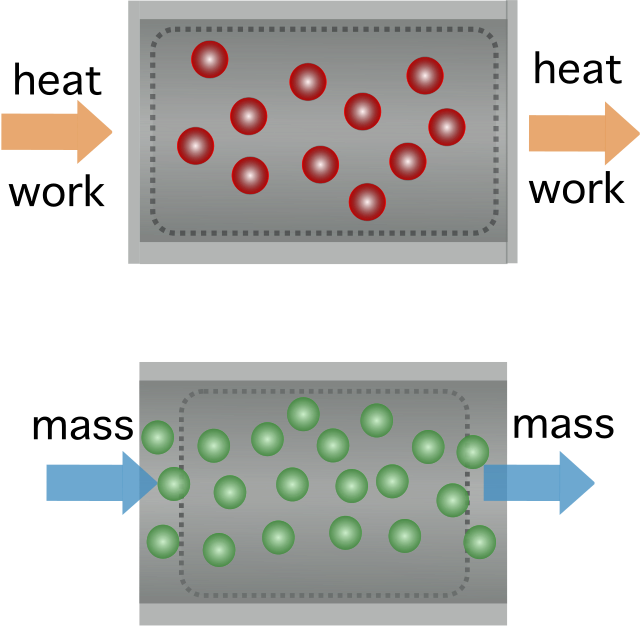
Figure 1. A non-flow process in thermodynamics is a process in which heat or work are exchanged (top) without there being any mass transfer (bottom). Source: Manuel R. Camacho, StudySmarter.
Processes that involve a mass flow can be divided into steady flow processes, in which there is a fixed amount of mass entering and leaving, and non-steady flow processes, in which there is a variable amount of mass leaving and entering.Reversible processes are those in which it is possible to return to the initial system properties, i.e., the initial temperatures, pressures, or volumes, without altering the system or its surroundings.
In the real world, all processes are non-reversible processes, which means that to return to the initial state of the system requires drawing energy or work from their surroundings.
Characteristics of non-flow processes
Non-flow processes have some other important characteristics apart from being closed:
- The thermodynamic state of gases can be defined by three variables: pressure, temperature, and volume.
- The processes allow gases to move from one state to another by changing one or more of these three variables.
- The processes keep one of the variables constant.
Non-flow processes in thermodynamics
The four states occurring in non-flow processes are known as isothermal, adiabatic, constant volume (isochoric or isometric), and constant pressure (isobaric).
Isothermal processes
During an isothermal process, the temperature keeps its value constant, while the pressure and volume change from one state to another, following Boyle’s Law. The product of both pressure (p) and volume (V) stays the same, and both variables follow the relationship shown in the formula below:
\[p_1V_1 = p_2V_2\]
Consider the following example.
A gas expands inside a circular balloon-type structure, increasing its volume twice from a pressure equal to 34 Pa in a sphere with a radius equal to 10 cm. Calculate the final pressure on the sphere wall if the change happens at a constant temperature.
First, we need to calculate the initial volume using the sphere volume formula:
\(V_1 = \frac{4}{3} \cdot \pi \cdot r^3 = \frac{4}{3} \cdot \pi \cdot (0.1)^3 = 4.18 \cdot 10^{-3} m^3 \approx 4.2 \cdot 10^{-3}m^3\)
Now we know the final volume is twice the initial one, V2 is equal to 2 times V1 as below:
\(V_2 = 2\cdot V_1 = 2 (4.2 \cdot 10^{-3} m^3) = 8.4 \cdot 10^{-3} m^3\)
If we then substitute the values in the isothermal equation, we get the new pressure:
\(p_2 = \frac{p_1V_1}{V_2} = \frac{4.2 \cdot 10^{-3} m^3}{8.4 \cdot 10^{-3}m^3} \cdot 34 Pa = 17 Pa\)
You could also solve this problem by expressing the formula in terms of the first volume:
\(p_2 = \frac{p_1V_1}{V_2} = \frac{p_1V_1}{2V_1} = \frac{p_1}{2}\)
In a process where the volume and pressure change, it is impossible to keep the temperature nearly constant. For this to happen, heat needs to be introduced into the reservoir slowly, i.e., at the same rate at which its temperature changes inside.
Another problem is that an isothermal process needs the gas and the section introducing heat to be at the same temperature, which, however, means that the heat cannot be conducted to the gas, and temperature cannot be kept constant.
However, in thermodynamics, if a material is a good heat conductor, the process can be considered isothermal.
Adiabatic processes
Adiabatic thermodynamic processes are those that feature no heat or mass transfer. By definition, non-flow processes do not exchange mass, but in these cases, there is also no heat transfer between the gas and the surroundings. In this case, the first law of thermodynamics dictates that the work done (W) by the gas must come from only its internal energy (U) change, as shown in the equation below:
\[\Delta U = W\]
Adiabatic processes thus can be expressed with the following equation:
\(p_1V_1^{\Upsilon} = p_2V_2^{\Upsilon}\)
Here, the exponent \(\Upsilon\) is a particular constant that is different for each gas.
Constant pressure processes
In a constant pressure or isobaric process, mechanical work is either made on or extracted from the gas. In these cases, work changes the volume of the gas while also modifying its temperature. A change in its temperature also involves a change in heat ‘Q’.
If we apply this to the definition of mechanical work as the change in volume, we can resolve this using the first law as follows:
\[Q = \Delta U + W\]
Here, ‘W’, which is the work done on the gas or by the gas (in which case it will be negative), is equal to the pressure ‘P’ per its volume change ‘ΔV’. This, in turn, is equal to the difference of the volumes Vf-Vi.
\[Q = \Delta U + (P \cdot \Delta V) = U + (P \cdot(V_f - V_i))\]
The final expression tells us how the heat in gas is related to the internal energy of the gas ΔU and the mechanical work done by or on it.
In this case, the work is equal to the pressure multiplied by the difference between the initial and final volume. Let us consider the example of a piston.
A piston with a radius of 10 cm produces a force of 10 N over a gas. The gas is in a 1 m long cylinder with a radius that is equal to the piston. It decreases the gas volume to 90% of its original value. Calculate the change in the internal energy if the gas increases its heat by 15 J.
We need to calculate the work done on the gas, so we need to multiply the pressure by the change of volume:
\[W = P \cdot (V_f - V_1)\]
We then calculate the pressure by using the area of the piston and the force exerted over it. In our example, the area of the piston is a circle with a 10 cm radius.
\[P = \frac{F}{A} = \frac{F}{\pi \cdot r^2} = \frac{10N}{\pi \cdot (0.1 m)^2} = 318.31 Pa \approx 318.3 Pa\]
Now, we calculate the final volume, knowing that it is 10% less than a cylinder whose height is 1 m and whose radius is equal to 10 cm. So we use the cylinder volume formula and multiply it by 0.9.
\(V_f = 0.9 \cdot (\pi \cdot r^2 \cdot h) = 0.9 \cdot (\pi \cdot (0.1m)^2 \cdot 1m) = 0.9 \cdot 0.031416 m^3 \approx 2.83 \cdot 10^{-2} m^3\)
We then solve the first law for the internal energy and substitute the values.
\(Q = \Delta U + P(V_f - V_i)\)![]()
\(\Delta U = Q - P(V_f - V_i) = 15 j -(318.3 Pa \cdot (2.83 \cdot 10^{-2} m^3 - 3.14 \cdot 10^{-2}m^3))\)
\(\Delta U = 15.98 j \approx 16 j\)
The result tells us that the internal energy increased as a consequence of the compression of the piston, which transmitted energy to the gas.
We can also solve the problem by multiplying the original volume by 0.1, which is the change in volume, as shown in the formula below.
\(\Delta U = Q - (W \cdot \Delta V) = Q - (W \cdot (0.1V_1))\)
In statistical thermodynamics, the heat in gas comes from the gas particles colliding with each other and moving rapidly. In the case of gas being compressed, it will heat up. This heat increase is proportional to the decrease in volume.
On the other hand, when a gas expands, it produces work and decreases its volume. The expansion increases the contact area of the gas. The work done also comes at the expense of energy and decreases the heat of the gas.
Constant volume processes
During a constant volume, i.e., an isochoric or isometric process, the gas does not experience a volume change, and if heat is injected into the system, it is spent in changing the internal energy of the gas. This is shown using the first law as follows:
\(\Delta U = Q\)
Non-Flow Processes - Key takeaways
- Non-flow processes are thermodynamic processes in which there is no exchange of mass.
- Non-flow processes can exchange heat or work with their surroundings.
- There are four types of thermodynamic non-flow processes, i.e., isochoric, isobaric, isothermal, and adiabatic processes.
- In isochoric processes, the volume does not change, in isobaric processes, the pressure does not change, in isothermal processes, the temperature does not change, and in adiabatic processes, there is no heat exchange.
Explanations 
Exams 
Magazine 
