Over the years, experiments, especially those conducted by Charles-Augustin de Coulomb, have shown that two or more electric charges exert a force on each other. One of the most interesting and important things about this force is that it is independent of the mass of the objects under study. To understand the quantities this force depends on, we have to study Coulomb’s law.
Coulomb’s law definition and equation
Coulomb’s law is a law of physics that states when two or more electrically charged objects are close enough to each other, they exert a force on each other. The magnitude of this force is proportional to the net charge of the particles and inversely proportional to the square of the distance between the particles under study.
This is how we write Coulomb’s law mathematically:
\[F = k \cdot \frac{|q_1 \cdot q_2|}{r^2}\]
F is the magnitude of the force between the charges, q1 and q2 are the charges measured in Coulombs, r is the distance between the charges measured in metres, and k is Coulomb’s constant with a value of 8.99 ⋅ 109 N·m2/C2.
The force is called the electrostatic force, and it is a vector quantity measured in Newtons.
Coulomb’s law: electrostatic force between two charges
It is important to note that there are two forces when two electric charges exert a force on each other. Take a look at the image below: the first force is the force that the first charge exerts on the second charge F12, and the second force is the force that the second charge exerts on the first charge F21. We know that like charges repel and unlike charges attract each other. In physics, this is none other than the electrostatic force itself.
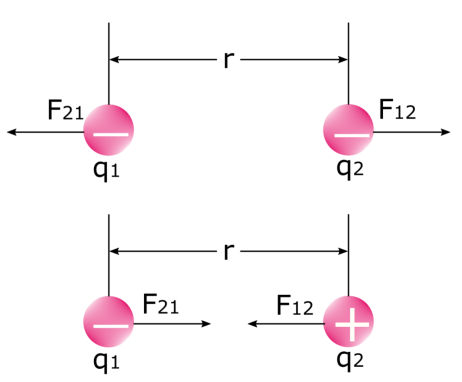
Like charges repel (above) and unlike charges attract each other (below)
It is important to know that the electric force F is not a constant. When charges exert forces on each other, they either come closer or push each other apart. As a result, the distance between them (r) changes, which affects the magnitude of the electric force between them.
For this explanation, we are looking into electrostatic forces, where “static” refers to the constant position for the source charges.
A hydrogen atom in its ground state consists of one electron and one proton. Calculate the force exerted on the proton by the electron if the distance between the two is 5.29 ⋅ 10-11 meters.
Solution
We know that electrons and protons have the same charge except with a different sign. In this example, we treat both the electron and proton as point charges. Let’s state the electron as q1 and the proton as q2.
\(q_1 = -1.602 \cdot 10^{-19}C \qquad q_2 = +1.602 \cdot 10^{-19}C\)
The distance between the two charges is also given in the question. Let’s put the known variables into Coulomb’s law.
\(F_{12} = 8.99 \cdot 10^9 N\cdot m^2/C^2 \cdot \frac{(1.602 \cdot 10^{-19} C)^2}{(5.29 \cdot 10^{-11}m)^2} = 8.24 \cdot 10^{-8}N\)
Since the charges are taken as point charges, the force the proton exerts on the electron will be the same. Thus, the direction of this force will be an attractive force (towards each other) since unlike charges attract.
Coulomb’s law: electrostatic force between multiple charges
We now know what happens when two charges exert forces on each other, but what happens when multiple charges exist? When there are multiple charges affecting one another, we must take two charges at a time into account.
The goal here is to find the net electrostatic forces these multiple charges exert on another point charge called the test charge. The reason behind this is to find the magnitude of the electrostatic force these multiple charges can provide. To find the net electrostatic force on the test charge, we use the principle of superposition. This principle allows us to calculate each charge’s individual electrostatic force on the test charge and then add these individual forces together as vectors. We can express this mathematically as follows:
\(\vec{F_{total}} = k \cdot Q \cdot \sum_{i = 1}^{N} \frac{q_i}{r_i^2}\)
In figure 2, given that q1 = 2e, q2 = -4e, the charge of the test charge is Q = -3e, and d = 3.0 ⋅ 10-8m, find the net electrostatic force exerted on the test charge Q.
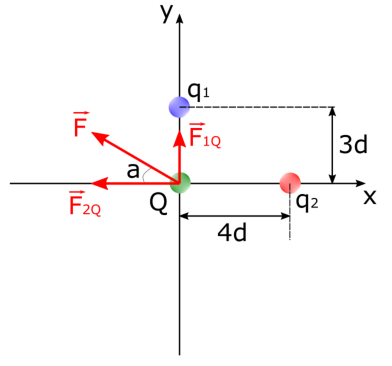
Diagram showing three point-like
particles exerting electrostatic forces on each other
Solution
Since the charges and distances between these charges are given in the question, we start by finding one of the force’s magnitude. Let’s find F2Q first.
\(|F_{2Q} = k \cdot \frac{|q_2 \cdot Q|}{(12 \cdot 10^{-8})^2} = 8.99 \cdot 10^9 N \cdot m^2/C^2 \cdot \frac{|(-6.408 \cdot 10^{-19} C)(-4.806 \cdot 10^{-19}C)}{1.44 \cdot 10^{-14}m} = 1.92 \cdot 10^{-13}N\)
Since q2 and Q are like charges, this force will be exerted on Q in the left direction on the x-axis. Now let’s find the magnitude of the electrostatic force exerted on Q by q1.
\(F_{1Q} = k \cdot \frac{|q_1 \cdot Q|}{(9 \cdot 10^{-8})^2} = 8.99 \cdot 10^9 N \cdot m^2/C^2 \cdot \frac{|(+3.204 \cdot 10^{-19}C)(-4.806 \cdot 10^{-19} C)|}{8.1 \cdot 10^{-15}m} = 1.71 \cdot 10^{-13}N\)
Since q1 and Q are unlike charges, this force will be in the up direction on the y-axis. We must add these two vectors together to find the net electrostatic force exerted on the charged particle Q. We can see that:
\(|\vec{F}| = \sqrt{|\vec{F_{1Q}}|^2 + |\vec{F_{2Q}}|^2}\)
If we put in the values we have found, we get:
\(|\vec{F}| = \sqrt{(1.92 \cdot 10^{-13} N)^2 + (1.71 \cdot 10^{-13}N)^2} = 2.57 \cdot 10^{-13} N\)
And to find the angle between the x-axis and the resultant force vector, we can find the tangent of the angle a.
\[\tan(a) = \frac{|\vec{F_{1Q}}|}{\vec{|F_{2Q}}|}\]
And if we solve for a, we get:
\[a = 41.69 ^\circ\]
Coulomb’s Law - Key takeaways
- Coulomb’s law is a law of physics that states when two or more electrically charged objects are close enough to each other, they exert a force on each other.
- The magnitude of this force is proportional to the net charge of the particles and inversely proportional to the square of the distance between the particles.
- The force charges exert on each other is called the electrostatic force.
- Like charges repel and unlike charges attract each other.
- When finding the resultant electrostatic force between multiple charges, we take two forces at a time and calculate their electrostatic forces. We then add all the forces together (as vectors) to find the resultant force.
Explanations 
Exams 
Magazine 
