The example of the bouncing ball is used to study projectile motion in mechanics.
Projectile motion is the motion of objects that are moving near the surface of the earth in a curved path due to the effect of gravity.
The example of the bouncing ball in physics
At the moment of impact, the ball also experiences deformation and the coefficient of restitution, which depends on the bounciness of the ball.
The push that the ball receives from the floor at the moment of the impact causes it to bounce upwards. The moving ball gains kinetic energy when it bounces, and loses potential energy as it falls.
Newton's third law states that every force or action has an equal and opposite reaction. Hence when a force is applied to a surface, it also applies a force equal in magnitude, but in the opposite direction.
The coefficient of restitution is the ratio of the final to initial speed between two bodies after the collision. While a value of 1 indicates a perfectly elastic collision, a value of 0 indicates a perfectly inelastic collision.
In the bouncing ball example, external forces such as air resistance are assumed to be zero. Hence, the only force acting on the ball is gravity. The motion of the ball can be split into different stages depending on the direction of the velocity vector; these stages are listed below. As a general rule, when the ball is travelling in the positive direction (upwards), the velocity can be assumed to be positive. When the ball travels in the negative direction (downwards), the velocity can be assumed to be negative. The positive and negative directions must be stated in each example.
The first stage is where the ball bounces from the surface of the ground. It travels upwards towards its highest point.
The second stage is the point at which the ball decelerates, changes direction once it has reached the peak point, and starts falling to the ground.
The third stage is the point at which the ball is momentarily deformed, and bounces off the ground in an upward direction until it reaches its maximum height.
The last stage is the point at which the ball has reached its maximum displacement, decelerates, and changes the direction of motion from upwards to downwards.
These stages are continuously repeated and shown in the sequence below. it seems the ball is experiencing an oscillatory motion. In reality, the ball experiences damping, where it loses potential energy and kinetic energy as it falls. This causes the amplitude of the height to reduce over time and eventually come to a stop due to friction forces like air resistance, which are assumed to be zero in an ideal scenario. The ball is not performing a simple harmonic motion, as the acceleration is not proportional to the displacement from an equilibrium position.
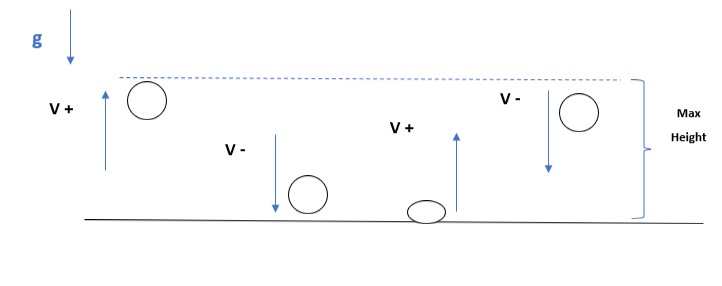
Stages of bouncing ball example, Panagi - StudySmarter Originals
(The upward direction was assumed to be positive in this example. This can either be assumed and chosen, or it can be stated in a question.)
At the point of maximum height, the ball momentarily has zero velocity, and the direction of velocity is changing from positive to negative. The acceleration on the ball is the acceleration of gravity, which acts downwards on the ball. At the lowest point, the ball has its minimum potential energy, and the velocity changes from negative to positive. These stages can also be represented graphically using three plots including a displacement, velocity, and acceleration vs time graph. These are illustrated below.
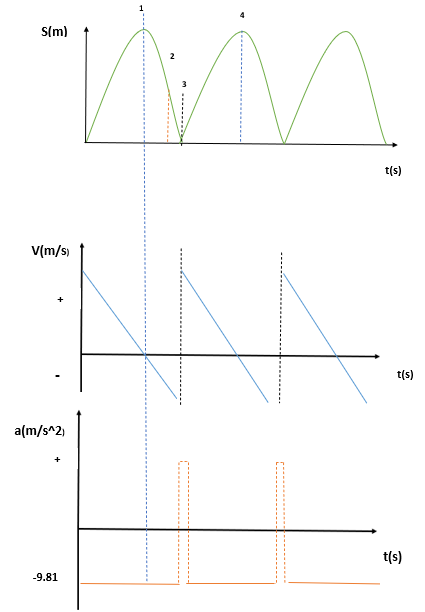
Motion graphs of a bouncing ball, Panagi - StudySmarter Originals
The first graph is a displacement vs time graph. The ball moves upwards, reaching stage 1, i.e., maximum height, and its velocity is momentarily zero. The acceleration due to gravity causes the ball to change direction and start moving downwards at stage 2.
Once the ball hits the ground, its displacement is momentarily zero. It bounces off, changing the direction of motion and again reaching its maximum height. This is also reflected in the velocity graph; the velocity is at its maximum at the minimum displacement and goes through zero at its maximum heights. The change in direction when the ball reaches the ground causes a momentary acceleration as seen in the acceleration graph (as acceleration).
- Potential energy causes a ball to impact the floor, which is then converted into kinetic energy and causes the ball to move upwards.
- The force that is received by the ball from the ground from the collision causes it to rebound, which converts the potential energy to kinetic energy. This phenomenon is described by Newton's third law.
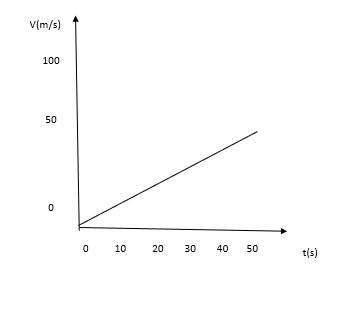
Velocity-time graph of a bouncing ball
A) Using the graph above, find the displacement of the ball at 50 seconds.
B) Using the conservation of energy, find the velocity of the ball before it hits the ground from a height of three metres.
Solution A:
Using the graph above, we can find the displacement by using the area under the graph, which is equal to the displacement. The area of the triangle can be found using the formula below.
\(Area = \frac{1}{2} \cdot base \cdot length\)
\(Area = 0.5 m \cdot 50 m \cdot 50 m = 1250 m^3\)
Solution B:
We use the conservation of energy. So, we equate the potential energy and the kinetic energy.
\(E_{pot} = E_{kin} \cdot m \cdot g \cdot h = \frac{1}{2} \cdot m \cdot v^2\)
The mass is cancelled out in the above equation, and we re-arrange with respect to velocity.
\(v^2 = 2 \cdot g \cdot hv = \sqrt{2 \cdot 9.81 \frac{m}{s^2} \cdot 3 m} = 7.67 \frac{m}{s}\)
What is a geometric sequence?
A geometric sequence is a progression where each term is related to the previous term, and it is related to the previous term by a number r, which is known as the common ratio of the sequence. The last term is also known as the nth term of a geometric progression; n is the number of terms and a is the first term while Sn is the sum of the terms in the sequence as shown in the equation below.
\[S_n = \frac{\alpha(1 -r^n)}{1-r}\]
For an infinite number of turns, another geometric sequence formula can be used. If the common ratio of the sequence is between 0 and 1, then the term r∞ would approach zero. Hence the formula for the sum of the infinite number of terms can be rewritten as seen here.
\[S_{\infty} = \frac{\alpha(1-r^{\infty})}{1-r} = \frac{\alpha(1-0)}{1-r} \qquad S_{\infty} = \frac{\alpha}{1-r}\]
Where 0 < r < 1
Relation of geometric sequence and a bouncing ball
A real-life bouncing ball example would experience an oscillatory motion which would gradually lose energy, causing the height of the bounce to reduce over time until eventually, the ball came to a stop.
This motion can be described using a geometric sequence, as the height of the ball after each bounce depends on the initial height from which the ball fell. The last term can be the lowest height of the ball before it comes to an end as seen below. Here, the motion of a real bouncing ball is shown. Its height gradually decreases until it eventually stops moving.
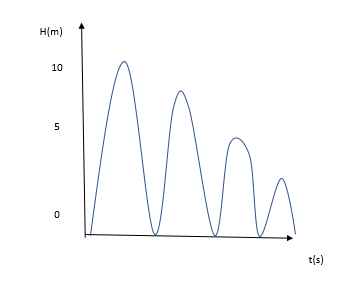
Height-Time graph of a bouncing ball
A ball falls from a height of 6 metres. The ball rebounds to 38 percent of its previous height and continues to fall.
A) Find the total distance of travel until the ball hits the ground for the 5th time.
B) If this is an ideal scenario where energy is not lost and the ball continues to bounce infinitely, what is the distance of travel?
Solution A:
Using the geometric sequence formula, the sum of the terms which are the heights of the ball after each bound:
\(S_n = \frac{\alpha(1-r^n)}{1-r} = \frac{6m(1-0.38^5)}{1-0.38} = 9.6 m\)
Finally, we need to multiply the distance found by 2, as one bounce of the ball includes both a rise and fall. Hence the final answer is:
\(\text{Total distance} = 2 \cdot S_n = 2 \cdot 9.6 m= 19.2m\)
Solution B:
Using the geometric sequence for an infinite sequence and substituting the given values we get:
\(S_{\infty} = 2 \cdot \frac{\alpha}{1-r} = 2 \cdot \frac{6m}{1-0.38} = 19.35 m\)
- A bouncing ball is an example of oscillatory motion as the ball is oscillating about the equilibrium position. It goes back to its initial vertical position after a period of time.
- A bouncing ball example is not an example of simple harmonic motion. Its high order and functions achieved with differential and integral operations can't fit any circle in simple harmonic motion; for it to qualify as simple harmonic motion, its speed would have to be constant.
Bouncing Ball Example - Key takeaways
- The bouncing ball example is an example used to study projectile motion in mechanics. It bounces in a semicircular trajectory, and obeys Newton's second law.
- The ball loses potential energy as it falls and gains kinetic energy as it moves and gains velocity.
- A bouncing ball in an ideal scenario will continue this oscillatory motion. In a real-life scenario, the ball will eventually stop moving due to external forces such as air friction.
- The motion of the ball can be described using velocity, displacement, and acceleration graphs, or geometric sequences.
Explanations 
Exams 
Magazine 
