What is power?
Power is the rate at which work is done per unit time. This is expressed mathematically as the work done W measured in J over time measured in seconds.
\[P[W] = \frac{W}{\Delta t}\]
Work done is a result of a force that displaces an object in the direction of the force. Its magnitude is given by the product of the force and the distance moved in the direction.
\[W[J] = F[N] \cdot x[m]\]
Therefore, Power can also be expressed as a factor of a force that is applied on an object and the displacement of the object using the formula above.
\[P[W] = \frac{W}{\Delta t} = \frac{F \cdot x}{\Delta t}\]
By substituting Work done by the product of a force and the object's displacement as done above, we get that power is equal to the product of force and rate of change of displacement x/Δt. On the other hand, the rate of change of displacement can be substituted by velocity v as seen below.
\[P = F \cdot \Delta \Big(\frac{x}{t} \Big) \qquad P = F[N] \cdot v[m/s]\]
Hence the power is also equal to the product of the force applied and the resulting velocity of the object.
A car of mass 800kg is travelling along a horizontal road. The car generates a power of 5kW. The total force of resistance for frictional force is 130N. What is the acceleration of the car when its speed is 10m / s?
Solution: Using Newton's second law we derive:
\[P = F \cdot v \Rightarrow F = \frac{P}{v}\]
Using the schematic below in figure 1, where Ft stands for friction force we use the sum of external forces to find the acceleration.
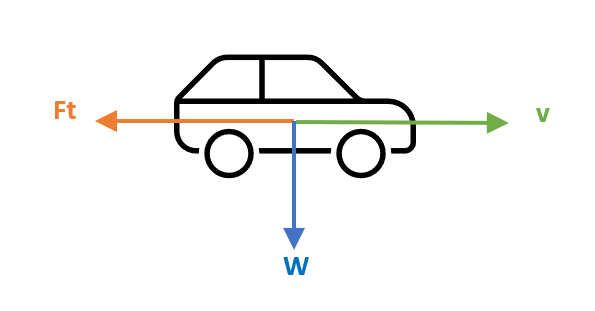
Figure 1.- Diagram showing the forces and velocity of the car
\[F = ma \qquad F_1 - F_t = ma \qquad \frac{5000}{10} - 130 = 800 \cdot aa = \frac{370}{800} m/s^2 = 0.4625 m/s^2\]
A 50kg student is travelling across a 10m long and 5m high incline with constant velocity as shown in the diagram below. Find the time it takes for the student to reach the end of the incline if the power output of the student is 1.3kW.
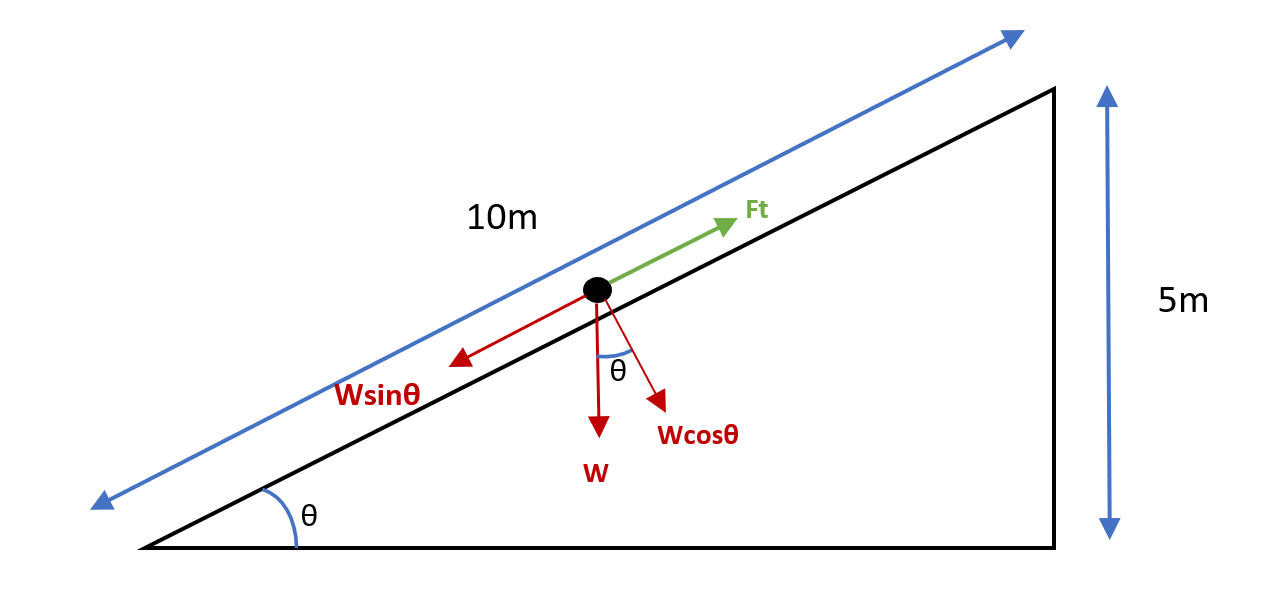
Figure 2.- Diagram showing the different forces on the student.
Solution:
We draw a diagram with an incline and the forces acting on the body. The velocity can be found by finding the rate of change of position over time. The time is unknown but the change of positions is known as the distance travelled is known, 10 m. The W force is divided into two vectors Wcosθ and Wsinθ so that the weight force components are in the same direction as the motion.
\[\sin \theta = \frac{5}{10} = 0.5 \qquad P = F \cdot v \qquad 1300 = F \cdot \frac{\Delta x}{\Delta t} \qquad 1300 = F \cdot \frac{10}{\Delta t}\]
Using Newton's second law, the sum of external forces is equal to zero since the velocity is constant, hence acceleration is zero. Let's name the force student applies F1. By substituting the given values we get.
\[F = ma, \space a = 0, \space F = 0 \qquad F_1 -W\sin \theta = 0 \qquad F_1 = m \cdot g \cdot \sin \theta \qquad F_1 = 50 kg \cdot 9.81 N/kg \cdot 0.5 = 245.25 N\]
Lastly using the equation for power we derived, we can now estimate the time required to travel the incline.
\[1300 = 245.25 \cdot \frac{10}{\Delta t} \qquad \Delta t = \frac{2452.5}{1300} s= 1.89 s\]
What is power factor and efficiency?
Power factor is a dimensionless quantity used in electrical engineering that describes the ratio between the true used power by a load measured in kW and the total power that flows through a circuit measured in kVA. Power factor has a range between -1 and 1 and can be expressed as a percentage. A negative power factor indicates that the voltage and current flowing through a circuit are not in phase.
- Real power or active power is the product between the voltage and current. It is used to express the capacity of electricity that performs work.
- Apparent power is the product of the RMS values of current and voltage.
\[P_f = \frac{P_R [KW]}{P_A [kVA]}\]
RMS or root mean square expresses the average current and voltage values in an AC system that is equivalent to the DC value that does the same amount of work. The RMS current and voltage are the maximum current and voltage over the squared root of two.
\[I_{rms} = I_{max}I\sqrt2 V_{rms} = V_{max} I\sqrt2\]
Relation between power and efficiency
Efficiency η is the dimensionless quantity that is used to express the amount of unused or wasted energy. It is a ratio of the used energy or output energy over the maximum theoretical energy or input energy. So what is the mathematical relationship between power and efficiency?
The efficiency can be expressed mathematically by the equation below where η is the efficiency expressed as a percentage, the Pout is the output power, the Pin is the input power both measured in kW.
\[\eta_{th} = \frac{P_{out}[kW]}{P_{in}[kW]} \text{ or } \eta_{\%} = \frac{P_{out}[kW]}{P_{out}[kW]} \cdot 100\]
The output power is always less than the input power as there is always some energy being lost due to friction, heat, etc. Therefore the efficiency will always be less than one in practice. The smaller the percentage of efficiency the greater the wasted energy. This can also be expressed mathematically in order to find the losses using the relation below.
\[\text{Maximum efficiency} = 1 \qquad P_{in}[W] = P_{out}[W] + \text{losses}[W]\]
The power factor is a measure of how efficiently electrical power is converted into useful work output and is also expressed as a percentage. Both power factor and efficiency can be used to express the amount of energy wasted.
Power and efficiency in engines
Power can also be used to express the power output of an engine, and it can be used to estimate the efficiency of an engine in terms of the amount of power that is used from the maximum available power input. This can be found using the following equations where PB is the brake power of an engine measured in W, and Pi is the power input from the fuel which can be found from the calorific value cf of the fuel and mass flow rate of the fuel m.
\[\eta_{th} = \frac{P_B[W]}{P_{in}[W]} \qquad P_{in} = m[kg/s] \cdot c_f[J/kg]\]
Find the thermal efficiency of an engine if the brake output is 35kW and the input power is 50kW.
Solution:
To calculate the thermal efficiency, we apply the above formula and substitute the given values.
\[\eta_{th} = \frac{35}{50} = 0.7 = 70 \%\]
Power and Efficiency - Key takeaways
- Power is the rate at which work is done per unit time or force multiplied by the velocity.
- Power factor is a dimensionless quantity that is used to express the wasted electrical energy.
- Power can also be used to express the power output of an engine and the efficiency of an engine in terms of the amount of power that is used from the maximum available power input.









