Centripetal force definition
Centripetal force is defined as the force required to keep an object moving in a circular path. The force acts towards the centre of rotation of the orbiting object.
The word centripetal means to seek the centre. All objects that move in a circular path need a net force acting towards the centre of rotation to keep them in orbit. We can see the effect of this force in our everyday lives.
The rotation of the earth around the sun is a good example that demonstrates the effects of the centripetal force due to gravity. This is provided by the pull of the sun's gravity, keeping the earth in an elliptical orbit and preventing it from getting lost in space, phew!.
 As you can see, there is a continuous change in the direction of the velocity vector during circular motion, this is known as directional acceleration, StudySmarter Originals
As you can see, there is a continuous change in the direction of the velocity vector during circular motion, this is known as directional acceleration, StudySmarter Originals
In a circular motion, the speed of the orbiting object does not change, only its direction. But then why do we say that a force is necessary for an object to move in a circular motion if the speed of the object is unchanging? In a circular motion, the direction of the velocity is constantly changing. This means any object moving in a circular path is undergoing directional acceleration. The acceleration does not change the magnitude of the velocity but only the direction of the velocity of the object. Acceleration can only be produced by an external unbalanced force. This force needed to constantly change the direction of an orbiting object the Centripetal force we speak about. Let us look at this reasoning in more detail as we determine how to calculate the centripetal force required to keep an object in a circular motion.
Centripetal force determination
Imagine a stone tied to a string that is being rotated at a uniform speed. Let the length of the string be, which is also the radius of the circular path. Now take a picture of this stone that is being rotated. What's interesting to note is that the magnitude of the tangential velocity of the stone will be constant at all points on the circular path. However, the direction of tangential velocity will keep changing. So what is this tangential velocity?
Tangential velocity is defined as the component of the velocity of an object at a given point in time, that acts in a direction that is tangential to the circle.
The tangential velocity vector points towards the tangent to the circular path followed by the stone. As the stone is being rotated this tangential velocity vector is constantly changing its direction.
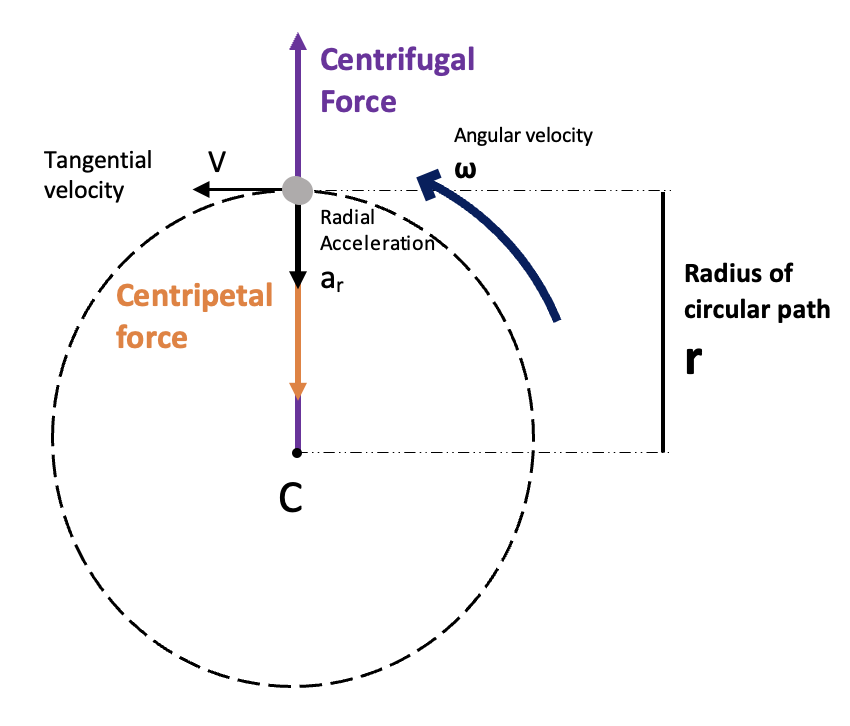
The centripetal force always acts towards the center of rotation, the force is the result of the directional acceleration acting on the body during circular motion, StudySmarter Originals
What does it mean when the velocity keeps on changing? The stone is accelerating and since only the direction is changing it's called directional acceleration. Now according to Newton's first law of motion, an object will continue to move in a straight line unless an external force acts on it. But what is this force that is making the stone move around in a circular path? You might recall when you spin the stone you're basically pulling the string. This creates tension in the string and this force will exert a pulling force on the stone. This is the force that is responsible for accelerating the stone towards you, and this force is known as the centripetal force.
The magnitude of a centripetal force or radial force is given by Newton's second law of motion
$$\overset{\mathit\rightharpoonup}{F_c}\mathit\;=\;m\overset{\mathit\rightharpoonup}{a_r}.$$
Where \(\overset{\mathit\rightharpoonup}{F_c}\) is the magnitude of the centripetal force, \(m\) is the mass of the object experiencing the centripetal force and \(\overset{\mathit\rightharpoonup}{a_r}\) is the centripetal acceleration. Every object moving in a circle has radial acceleration. This radial acceleration can be represented as
$$\overset\rightharpoonup{a_r}=\frac{v^2}r$$
$$\text{radial}\;\text{acceleration}\;=\;\frac{\text{tangential}\;\text{velocity}}{\text{radius}\;\text{of}\;\text{circular}\;\text{path}}$$
Add this to the equation for centripetal force and we get $$\overset\rightharpoonup{F_c}=\frac{mv^2}r.$$
The centripetal force will always act perpendicular to the tangential velocity. This is how this force is able to continuously alter the direction of the object towards the centre. The tangential velocity can also be represented as :
$$v=r\omega$$ $$\mathrm{Tangential}\;\mathrm{velocity}=\mathrm{radius}\;\mathrm{of}\;\mathrm{circular}\;\mathrm{path}\times\;\mathrm{angular}\;\mathrm{velocity}$$
Substituting this for velocity into the equation for the centripetal force provides us with another equation for centripetal force in terms of angular velocity: $$\overset\rightharpoonup{F_c}=mr\omega^2$$ $$\text{centripetal}\;\text{force}\;=\;\text{mass}\times\text{radius}\times\text{angular}\;\text{velocity}^2$$
where mass is measured in \(\mathrm{kg}\), radius in \(\mathrm m\) and angular velocity, \(\omega\) in \(\text{radians}/\text{sec}\). Let's now use these equations in a few examples.
We will need to convert the unit for angular velocity from degrees/ sec into radians/ sec before using it in the above equation. This can be done using the following equation \(\text{Deg}\;\times\;\pi/180\;=\;\text{Rad}\) .
According to Newton's third law of motion, every action will have an equal and opposite reaction. So then what could possibly act in the opposite direction of centripetal force.
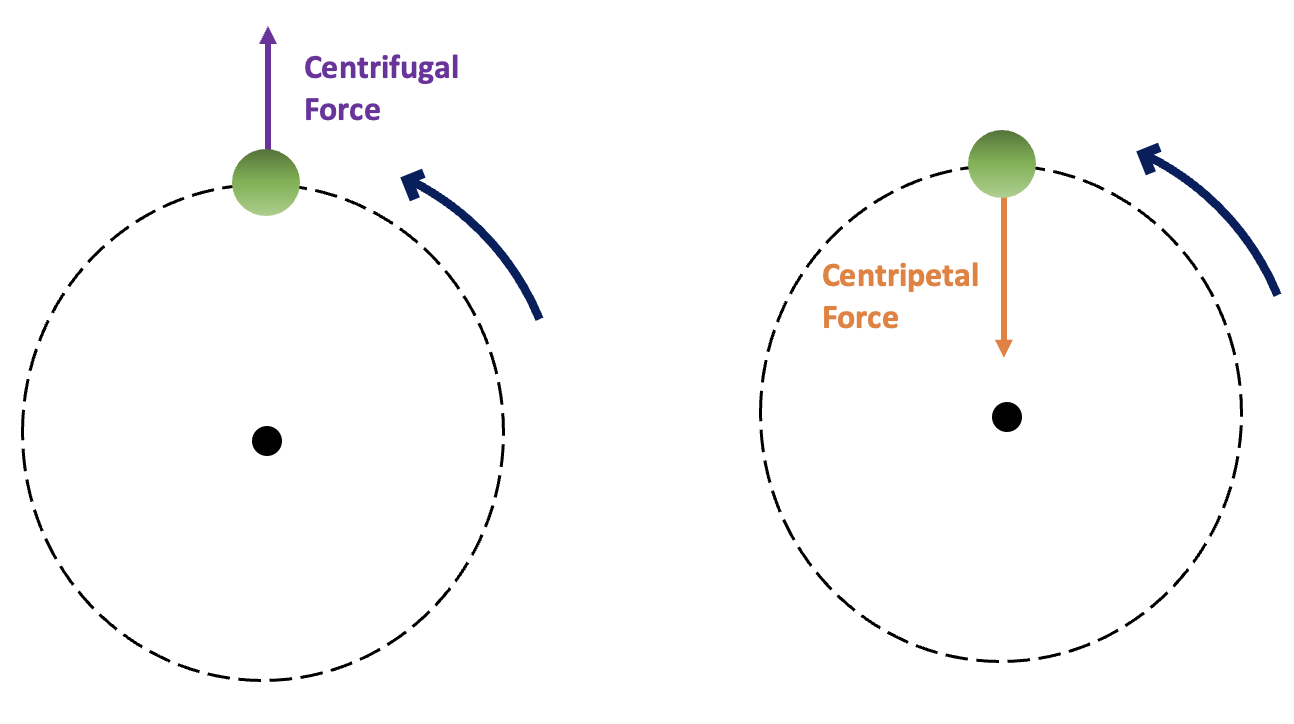
Centrifugal force will always act in the opposite direction that is away from the center of rotation, StudySmarter Originals
Centrifugal force is a pseudo force experienced by an object that moves in a curved path. The direction of the force acts outwards from the centre of the rotation.
Centripetal Force equation
Let's take a closer look at the equation for centripetal force. The centripetal force required to keep an object of mass\(m\) in a circular motion of radius \(r\) with an angular velocity of \(\omega\) is given by $$\overset{\mathit\rightharpoonup}{F_c}\mathit\;=\;mr\omega^{\mathit2}$$
As you can see from the above equation, the magnitude of the centripetal force depends on the mass of the body. The greater the mass, the greater the force required to keep the object in a circular motion. It is important to make the distinction between mass and weight here. The mass of the body is always the same. The effect of a gravitational field on mass is what we experience as weight.
Centripetal force examples
A \(100\;\mathrm g\) ball, attached to the end of a string, is spun around in a circle with an angular speed of \(286\;\mathrm{degrees}/\sec\). If the string's length is \(60\;\mathrm{cm}\), Calculate the centripetal force required to keep the ball in a circular motion.
Step 1: Write down the given quantities. $$m=100\;\mathrm g,\;\omega=286\;\deg/\sec,\;r=60\;\mathrm{cm}$$
Step 2: Convert units.
Converting degrees into radians. $$\mathrm{Radians}=\mathrm{Deg}\;\times\;\mathrm\pi/180\;$$ $$=286\;\times\mathrm\pi/180$$ $$=5\;\text{radians}$$
Hence \(286\;\text{degrees}/\text{second}\) will be equal to \(5\;\text{radians}/\text{second}\).
Converting centimetres into meters $$1\;\mathrm{cm}\;=\;0.01\;\mathrm m$$ $$60\;\mathrm{cm}\;=\;0.6\;\mathrm m$$
Step 3: Calculate centripetal force using angular velocity and radius.
Using the equation $$F\;=\;\frac{mV^2}r\;$$ $$F\;=\;m\;\omega^2\;r$$ $$F\;=100\;\mathrm g\times5^2\;\mathrm{rad}^2/\sec^2\times0.6\;\mathrm m$$ $$F\;=\;125\;\mathrm N$$
The centripetal force required to keep a ball of the above specifications in circular motion is equal to \(125\mathrm N\).
This brings us to the end of this article, let's look at what we've learned so far.
Centripetal Force - Key takeaways
- Centripetal force is defined as the force required to keep an object moving in a circular path. The force acts towards a point called the center of rotation.
- Centripetal force is the force that allows an object to rotate around an axis.
- The centrifugal force is equal to the magnitude of the centripetal force but acts in the opposite direction.
- The equation for centripetal force is given by \(\overset\rightharpoonup{F_c}=\frac{mv^2}r\).
- Always remember that the unit for angular velocity while using the above equation must be in \(\text{radians}/\text{sec}\).
- This can be done using the following conversion factor \(\mathrm{Radians}=\mathrm{Deg}\;\times\;\mathrm\pi/180\) .
- The centripetal force will always act perpendicular to the tangential velocity. This is how this force is able to continuously alter the direction of the object towards the center.










