Angular Motion and Linear Motion: Definitions

Q: What characterizes linear motion and angular motion?

Linear motion is characterized by linear kinematic variables and equations while angular motion is characterized by angular kinematic variables and equations.

Angular Motion and Linear Motion Definitions

Motion is the action of an object moving or being moved. Motion can be classified in terms of linear motion or angular motion.

Linear motion is a one-dimensional motion along a straight path.

In contrast, angular motion deals with a curved path.

Angular motion is the circular motion about a fixed axis.

Angular Motion and Linear Motion Relationship

Angular motion and linear motion are related by a field in physics known as kinematics.

Kinematics refers to the study of motion without considering the forces at play.

In the field of kinematics, there are four corresponding quantities of motion. These quantities are

Velocity
Acceleration
Displacement
Time

and can be written in terms of linear or angular motion. The motion variables above correspond to linear motion.

Note that velocity, acceleration, and displacement are all vector quantities meaning they have magnitude and direction.

Linear Motion Variables

Let us define each linear motion quantity starting with displacement.

Displacement, $ x $, is the difference between an initial and final position along a specified path.

The mathematical formula corresponding to this definition is $$x=v\,\Delta{t}$$ where $ v $ is velocity and $ t $ is time. Displacement has an SI unit of $\mathrm{m}$. Displacement is sometimes confused with the term distance. Displacement is the overall change in an object’s position while distance is the magnitude of displacement.

Velocity, $ v $, is the rate of an object's change in displacement with respect to time.

The mathematical formula corresponding to this definition is

$$v=\frac{\Delta{x}}{\Delta{t}}$$ where $ x $ is displacement and $ t $ is time. Velocity has a SI unit of $ \mathrm{\frac{m}{s}} $. However, for instantaneous velocity we use $ v=\frac{dx}{dt}. $ Again, just as displacement is confused with distance, velocity is confused with speed. Velocity is the directional rate of change in position while speed is the magnitude of velocity.

Acceleration, $ a $, is an object's change in velocity with respect to time.

The mathematical formula corresponding to this definition is

$$a=\frac{\Delta{v}}{\Delta{t}}$$ where $ v $ is velocity and $ t $ is time. Acceleration has a SI unit of $ \mathrm{\frac{m}{s^2}}. $ However, for instantaneous acceleration, we use $ a=\frac{dv}{dt}. $

Time, $ (t) $ does not change relative to an object's type of motion and is measured in $ s. $

Angular Motion variables

For angular motion, the four quantities of motion are

angular displacement - The angle that an object moves through relative to some center of rotation.
angular velocity
angular acceleration
time

Now, let us define each variable starting with angular displacement.

Angular displacement, $ \theta $, is difference between an initial and final angular position around a specified axis.

The mathematical formula corresponding to this definition is $$\theta=\omega\,\Delta{t}$$ where $ \omega $ is angular velocity and $ t $ is time. Angular displacement has an SI unit of $\mathrm{radians}$.

Angular velocity, $ \omega $, is the rate of an object's change in angular displacement with respect to time.

The mathematical formula corresponding to this definition is

$$\omega=\frac{\Delta{\theta}}{\Delta{t}}$$ where $ \theta $ is angular displacement and $ t $ is time. Angular velocity has a SI unit of $ \mathrm{\frac{rad}{s}} $.

The derivative of this equation yields $ \omega=\frac{d\theta}{dt} $ , which is the definition of instantaneous angular velocity.

Angular acceleration, $ \alpha $, is an object's change in angular velocity with respect to time.

The mathematical formula corresponding to this definition is

$$\alpha=\frac{\Delta{\omega}}{\Delta{t}}$$ where $ \omega $ is angular velocity and $ t $ is time. Angular acceleration has a SI unit of $ \mathrm{\frac{rad}{s^2}} $.

The derivative of this equation yields $ \alpha=\frac{d\omega}{dt} $ , which is the definition of instantaneous angular acceleration.

Time, $ (t) $ does not change relative to an object's type of motion and is measured in $ s. $

Relationship between Motion Variables

Besides understanding the definitions and corresponding formulas for linear motion quantities and angular quantities, we should also be aware of the relationship between these quantities. Velocity is the first derivative of displacement with respect to time, $ v=\frac{dx}{dt} $, while acceleration is the first derivative of velocity with respect to time, $ a=\frac{dv}{dt} $ as well as the second derivative of displacement $ a=\frac{d^2{x}}{dt^2}. $ Likewise, angular velocity is the first derivative of angular displacement with respect to time, $ \omega=\frac{d\theta}{dt} $, while angular acceleration is the first derivative of angular velocity with respect to time, $ \alpha=\frac{d\omega}{dt} $ as well as the second derivative of angular displacement $ \alpha=\frac{d^2\theta}{dt^2}. $ Lets check our understanding with the following two examples, starting with angular motion.

Given the position function, $ x(t)=\left(9\;\mathrm{\frac{m}{s^2}}\right) t^2 +\left(6\;\mathrm{\frac{m}{s^2}}\right)t -4\;\mathrm{m}, $ calculate the velocity and acceleration functions.

Solution

To find the velocity function we can calculate the derivative of the position function with respect to time.

\begin{align}v(t)&=\frac{\mathrm{d}x}{\mathrm{d}t}\\v(t)&= \frac{\mathrm{d}}{\mathrm{d}t} \left( \left(9;\mathrm{\frac{m}{s^2}}\right) t^2 +\left(6\;\mathrm{\frac{m}{s}}\right)t -4\;\mathrm{m}\right)\\v(t)&=\left(18\;\mathrm{\frac{m}{s^2}}\right)t+6\;\mathrm{\frac{m}{s}}\end{align}

Similarly, since acceleration is the second derivative of the position function, we can find it by calculating the derivative of the velocity function.

\begin{align}\\a(t)&=\frac{\mathrm{d}v}{\mathrm{d}t}\\a(t)&= \frac{\mathrm{d}}{\mathrm{d}t} \left(\left(18\;\mathrm{\frac{m}{s^2}}\right)t+6\;\mathrm{\frac{m}{s}}\right)\\a(t)&=18\;\mathrm{\frac{m}{s^2}}\\\end{align}

One more time for angular motion.

Given the angular position function, $ \theta(t)=\left(5\;\mathrm{\frac{rad}{s^2}}\right) t^2 +\left(8\;\mathrm{\frac{rad}{s^2}}\right)t -6\;\mathrm{rad}, $ calculate the angular velocity and angular acceleration functions.

Solution

To find the angular velocity function we can calculate the derivative of the angular position function with respect to time.

\begin{align}\omega(t)&=\frac{\mathrm{d}\theta}{\mathrm{d}t}\\\omega(t)&= \frac{\mathrm{d}}{\mathrm{d}t} \left( \left(5\;\mathrm{\frac{rad}{s^2}}\right) t^2 +\left(8\;\mathrm{\frac{rad}{s}}\right)t -6\;\mathrm{rad}\right)\\\omega(t)&=\left(10\;\mathrm{\frac{rad}{s^2}}\right)t+8\;\mathrm{\frac{rad}{s}}\end{align}

Similarly, since angular acceleration is the second derivative of the angular position function, we can find it by calculating the derivative of the angular velocity function.

\begin{align}\\\alpha(t)&=\frac{\mathrm{d}\omega}{\mathrm{d}t}\\\alpha(t)&= \frac{\mathrm{d}}{\mathrm{d}t} \left(\left(10\;\mathrm{\frac{rad}{s^2}}\right)t+8\;\mathrm{\frac{rad}{s}}\right)\\\alpha(t)&=10\;\mathrm{\frac{rad}{s^2}}\\\end{align}

Now that we understand the relationship between the quantities themselves, we also need to discuss how linear motion quantities and angular motion quantities are related to one another. These relationships appear in the table below, where $ r $ is the radius of the circular motion.

Variable	Linear Abbreviation	Linear SI units	Angular Abbreviation	Angular SI units	Relationship
acceleration	$$a$$	$$\frac{m}{s^2}$$	$$\alpha$$	$$\frac{rad}{s^2}$$	$$a=\alpha{r}, \alpha=\frac{a}{r}$$
velocity	$$v$$	$$\frac{m}{s}$$	$$\omega$$	$$\frac{rad}{s}$$	$$v=\omega{r}, \omega=\frac{v}{r}$$
displacement	$$x$$	$$m$$	$$\Delta \theta$$	$$rad$$	$$x=\theta{r}, \theta=\frac{x}{r}$$
time	$$t$$	$$s$$	$$t$$	$$s$$	$$t=t$$

To better understand these relationships, let us look at the diagram below.

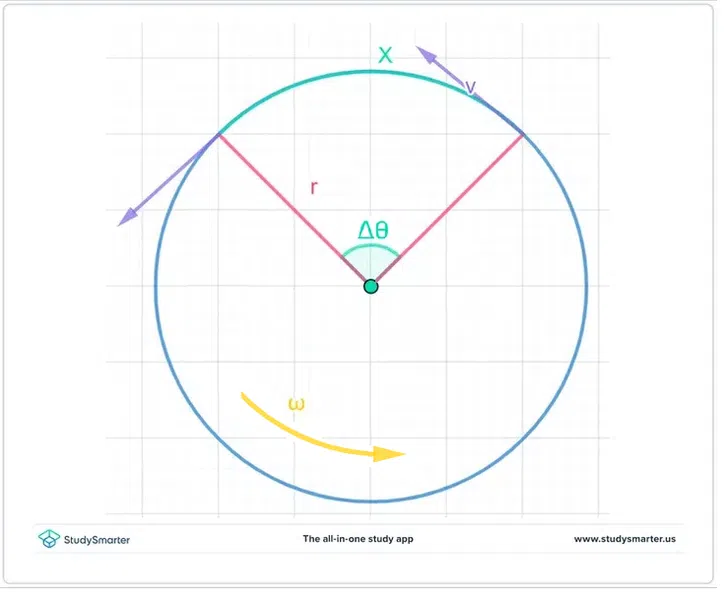
Rotational Dynamics Relationship Diagram StudySmarter

Fig. 1 - A diagram illustrating the relationship between linear kinematic variables and angular kinematic variables where $ v=\text{velocity},$ $r=\text{radius},$ $ X=\text{linear displacement},$ $ \Delta \theta=\text{angular displacement},$ and $ \omega=\text{angular velocity.} $

Angular displacement, $\theta$ is a measurement of how much a body has revolved around a specified axis, given as an angle usually in units of radians. Angular displacement is directly related to linear displacement, as linear displacement concerns the straight-line distance between points while angular displacement concerns the curved motion path between these points. Linear displacement is proportional to the radius of rotation and angular displacement. Tangential velocity, $v$ describes the instantaneous linear component of an object's motion relative to its circular path in the direction perpendicular to the normal to the direction to the centre of rotation. A way to visualize this is to imagine spinning a mass on a string - if we cut the string, the mass will continue moving with its tangential velocity at the instant the string was severed. This direction is perpendicular to the centre of the circle of rotation of the mass.

Similarly, this relationship describes the relationship between angular acceleration and linear acceleration. If we insert the formula for angular velocity, $ \omega=\frac{v}{r} $, into the equation for angular acceleration, $ \alpha=\frac{\Delta{\omega}}{\Delta{t}} $, we can derive the corresponding equation that relates angular acceleration to the instantaneous linear acceleration, $ \alpha=ar. $ Linear motion quantities are analogous to angular motion quantities.

Angular Motion and Linear Motion Equations

Consequently, three equations describe the relationship between linear and angular motion quantities. These equations are known as the "Big Three" and are two distinct sets of equations used to calculate unknown kinematic variables. Each equation is missing a single kinematic variable. As a result, when choosing what equation is necessary to solve a problem, determine which variable is not provided and what variable is not asked to be found.

Linear Motion Kinematic Equations

The velocity equation,

$$v=v_{o} + a{t}.$$

The displacement equation,

$$\Delta{x} =v_o{t}+\frac{1}{2}{a}t^2.$$

The velocity squared equation,

$$v^2={v_{o}}^2 +2{a}\Delta{x}.$$

Note that $ v $ is final velocity, $ v_o $ is the initial velocity, $ a $ is acceleration, $t$ is time, and $\Delta{x} $ is displacement.

These kinematic equations only apply when acceleration is constant.

Let's do a quick example to check our understanding.

A swimmer, anticipating the signal to go, waits on the starting block. When signaled to go, they dive into the water and begin swimming with a velocity of $ 0\,\mathrm{\frac{m}{s}}. $ The swimmer accelerates until they reach a speed of $ 2.7\,\mathrm{\frac{m}{s}}. $ What is the acceleration of the swimmer and displacement over this acceleration if it takes $ 30\,\mathrm{s} $ to reach the final speed?

Angular Motion and Linear Motion Relationship Swimmer StudySmarter Fig. 2: A swimmer demonstrates linear motion.

Based on the problem, we are given the following: initial velocity, final velocity and time. As a result, we can identify and use the equation,$ v=v_o + at, $ to solve part one of this problem. Therefore, our calculations are:

\begin{align}v&=v_o + at\\2.7\,\mathrm{\frac{m}{s}}&= 0 + a\,(30\,\mathrm{s})\\a&= \frac{2.7\,\mathrm{\frac{m}{s}}}{30\,\mathrm{s}}\\a&=0.09\,\mathrm{\frac{m}{s^2}}\\\end{align}

Using this value and equation, $ v^2=v_{o}^2 +2a\Delta x, $ we can calculate the swimmer's displacement as follows: \begin{align}v^2&=v_{o}^2 +2a\Delta x\\\left({2.7\,\mathrm{\frac{m}{s}}}\right)^2&=0 +2\left(0.09\,\mathrm{\frac{m}{s^2}}\right){\Delta x}\\7.29&=(0.09)(\Delta x)\\\Delta x&= \frac{7.29}{0.09}=81\,\mathrm{m}\\\end{align}

Angular Motion Kinematic Equations

The following equations represent the kinematic equations for angular motion for an object moving with constant angular acceleration.

The angular velocity equation is given by

$$\omega=\omega_{o} + \alpha{t}.$$

The angular displacement equation is given by

$$\Delta{\theta} =\omega_o{t}+\frac{1}{2}{\alpha}t^2.$$

The angular velocity squared equation is given by

$$\omega^2={\omega_{o}}^2 +2{\alpha}\Delta{\theta}.$$

Note that $\omega$ is final angular velocity, $\omega_0$ is the initial angular velocity, $\alpha$ is angular acceleration, $t$ is time, and $\Delta \theta$ is angular displacement.

These kinematic equations only apply when angular acceleration is constant.

Again, let's complete another example using the angular motion equations.

A fan initial rotates with an angular velocity of $ 1.6\,\mathrm{\frac{rad}{s}}. $ If its angular acceleration is $ 2.1\,\mathrm{\frac{rad}{s^2}} $ and the angular displacement of one of its blades over this acceleration is $ 7.3\,\mathrm{rad}, $ what is the fan's final angular velocity?

Angular Motion and Linear Motion Relationship Fan StudySmarter Fig. 3: A fan demonstrates angular motion.

Based on the problem, we are given the following: initial angular velocity, angular acceleration and angular displacement. As a result, we can identify and use the equation, $ \omega^2=\omega_{o}^2 +2\alpha\Delta\theta, $ to solve this problem. Our calculations are as follows:

\begin{align}\omega^2&=\omega_{o}^2 +2\alpha\Delta\theta \\\omega^2&=\left(1.6\,\mathrm{\frac{rad}{s}}\right)^2 +2\left(2.1\,\mathrm{\frac{rad}{s^2}}\right)(7.3\,\mathrm{rad})\\\omega^2&= 33.22\\\omega&= 5.8\,\mathrm{\frac{rad}{s}}\\\end{align}

Angular Motion and Linear Motion Similarities

Similarities between angular motion and linear motion can be seen in their corresponding motion variables and kinematic equations. Although, variables change, and each describes a different type of motion, the relationship between displacement, velocity, and acceleration remains the same regardless of motion. Why? Well, this is the result of velocity being the first derivative of displacement and acceleration being the first derivative of velocity and the second derivative of displacement. Regardless of motion and the path taken, these derivatives hold true when acceleration is constant. Therefore, we consider angular motion to be analogous to linear motion which results in angular motion and linear motion variables being equivalent counterparts to one another. As a result, the kinematic equations corresponding to each set of variables are analogous as well.

Angular Motion and Linear Motion Differences

Although similar, linear motion is characterized by linear kinematic variables and equations, while angular motion is characterized by angular kinematic variables and equations. Each describes a different form of motion and has different units of measure. Linear motion describes the motion of objects along a straight path and its associated variables are measured in units of length. Angular motion is the circular motion of objects about a fixed axis and its associated variables are measured in angular units such as radians or degrees. However, two distinct differences between angular motion and linear motion involve the force causing the motion and the coordinate system used to analyze each type of motion. Force causes linear motion while torque causes angular motion. As a result, two different coordinate systems can be used. For linear motion, we use the typical Cartesian coordinate system, $ x,y, $ however, for angular motion a polar coordinate system is better suited.

The polar coordinate system is a two-dimensional coordinate system in which the positions of points are defined in terms of the angle from some axis and the distance from a central point.

In this type of coordinate system, we use $ \rho,\theta, $ where $ \rho $ is the distance between the object and the origin and $ \theta $ is the angle between the x-axis and the position vector that gives us the direction. We can transform from a cartesian coordinate system to a polar coordinate system by understanding that $ x=\rho\cos\theta, $ $ y=\rho\sin\theta,$ and $\rho = \sqrt{x^2 +y^2}.$

Angular Motion and Linear Motion - Key takeaways

Linear motion is a one-dimensional motion along a straight path.
Angular Motion is rotational motion about a fixed axis.
Angular motion and linear motion are related by a field in physics known as kinematics.
Kinematics focuses on motion and how the variables of motion depend on each other.
Linear motion corresponds to acceleration, velocity, displacement, and time as well as 3 kinematic equations.
Angular motion corresponds to angular displacement, angular velocity, angular acceleration, and time as well as 3 kinematic equations.
Velocity is the first derivative of displacement with respect to time, $ v=\frac{dx}{dt} $, while acceleration is the first derivative of velocity with respect to time, $ a=\frac{dv}{dt} $ as well as the second derivative of displacement $ a=\frac{d^2{x}}{dt^2}. $
Angular velocity is the first derivative of angular displacement with respect to time, $ \omega=\frac{d\theta}{dt} $, while angular acceleration is the first derivative of angular velocity with respect to time, $ \alpha=\frac{d\omega}{dt} $ as well as the second derivative of angular displacement $ \alpha=\frac{d^2\theta}{dt^2}. $
Linear motion quantities are analogous to angular motion quantities.
Linear motion and angular motion are two different forms of motion, each with different units of measure.

References

Fig. 1: Linear and Angular Kinematic Relationship Diagram- StudySmarter Originals
Fig. 2: Swimmer (https://www.pexels.com/photo/person-swimming-on-body-of-water-863988/) by Guduru Ajay bhargav ( https://www.pexels.com/@ajaybhargavguduru/) is licensed by CC0 1.0 Universal (CC0 1.0).
Fig. 3: Fan-StudySmarter Originals

Angular Motion and Linear Motion

StudySmarter Editorial Team

Angular Motion and Linear Motion Definitions